〜終わり〜
■ぜひアンケートにご協力下さい■


電磁誘導現象は電気のあるところであればどこにでも現れる現象である。このシリーズは電磁誘導現象とその扱い方について解説する。今回は、電磁誘導現象とはどんな現象なのかについて、いろいろな事例を取り上げながら理解を深める。
この講座をご覧いただくには、Adobe Flash Player が必要です。
Adobe Flash Playerはこちらから無料でダウンロードできます。
私たちの身近にある磁石には両端に磁極があり、磁極と磁極の間には、力が働く(磁気のクーロンの法則による)。この力を磁気が原因で作用する力と云い磁気力と呼ぶ。したがって、磁極が存在する周囲の空間は、他に磁極があると想定すれば、磁気力が働く空間を意味するので、このような空間を磁界という。ある点の磁界は、その点で単位正磁極が受ける磁気力の大きさと、その磁極が受ける力の方向で表し磁界の強さ(大きさ、方向)で表す。そして磁界の強さは磁力線という方向をもった線(指力線)で視覚的に表現する(磁力線:磁界の大きさ=線密度、磁界の方向=線の接線方向)。磁石には正負の2種類の磁極が常に1対で存在する。例えば、第1図に示す棒状磁石(N極が青、S極が白)がつくる磁界の模様は磁力線で表すと図のようになる。
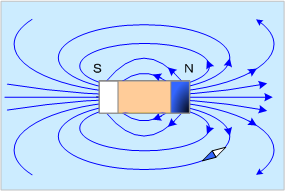
第1図 磁石のつくる磁界
第2図(a)に示す磁針を、同図(b)のように磁界中に置くと、磁針は磁界の方向を向く。このため、第1図の場合、磁針を図の位置に置くと、磁針は磁力線の接線方向を向く。このように、磁針を使うことによって、いろいろな磁界の様子を調べることができる。
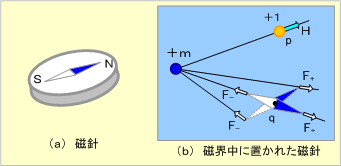
第2図 磁針を使うと磁界の方向がわかる
エルステッドは導線に電流が流れるとその周囲に磁界ができることを発見した。
(1)直線電流が作る磁界
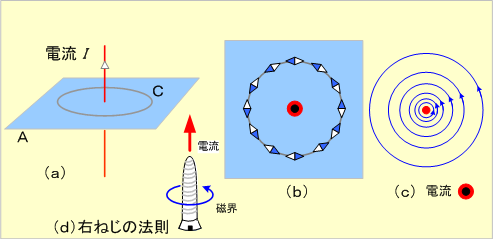
第3図 直線電流のつくる磁界
第3図(a)に示す非常に長い直線導体に図の方向に電流を流すと、電流に直角の平面A上で電流を中心とした円周Cには同図(b)のように磁針が並ぶ。
この時の磁界の大きさHは、電流をI〔A〕、電流からの距離をr〔m〕とすれば、
であることが知られている。このことから、同図(c)のように電流に垂直な平面上に、電流を中心とした同心円状の磁界ができ、磁力線は図のように電流に近いところほど密になる。電流と磁界との方向の関係は、同図(d)の右ねじの法則で知ることができる。
(2)円形電流が作る磁界
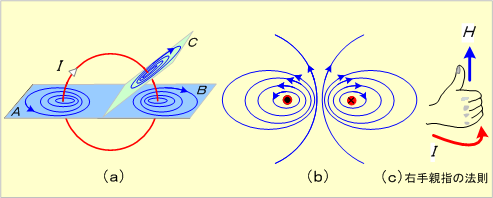
第4図 円形電流のつくる磁界
第4図(a)のような円の円周に沿って時計方向に電流Iを流すと、電流に垂直な平面ABC上に図示の磁界ができる。この磁界は何れの平面でも同一で、例えばAB平面では上から見た磁界は図(b)のようになる。したがって,このような磁界が円の中心を含む各面にでき、円形電流全体としての磁界は第5図(a)となる。このため、この磁界は同図(b)のように厚さの非常に薄い板状の磁石がつくる磁界と酷似したものとなる。
この円形電流がつくる磁界Hは、電流をI〔A〕、半径を
![]()
![]() 〔m〕とすれば、円の中心では、
〔m〕とすれば、円の中心では、
であり、電流と磁界との関係は、同図(c)に示す右手親指の法則によって知ることができる。
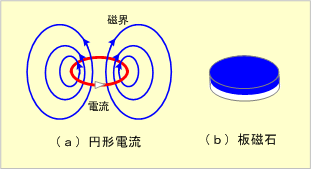
第5図 円形電流のつくる磁界
(3)ソレノイドが作る磁界
円筒の表面に沿って電線を螺旋状に巻いたものをソレノイド(以下、単にコイルと呼ぶ)という。第6図(a)のように線を密に巻いたコイルに電流を流した場合の磁界は、円形電流が横に並んでいると見なせるので、例えば2個の円形電流がつくる磁界は同図(b)のようになる。したがって、n回巻きのコイルではこの円形電流がn個並んでいることになるので、その磁界は同図(c)のようになる。このため、この磁界はコイルの端面に磁極をもつ磁石のつくる磁界に似ている。この場合の電流と磁界との関係は円形電流と同様に右手親指の法則で知ることができる。
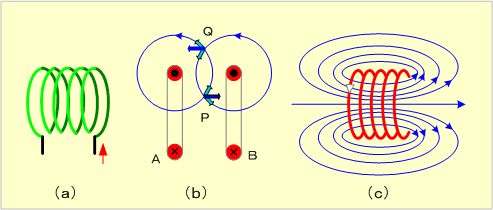
第6図 コイルがつくる磁界
(4)磁界の表し方
これまで磁界は磁力線によって表してきた。磁力線は、直線電流や円形電流の場合は閉じた線であるが、磁石のような場合は、第1図のように発生や消滅があるなど取り扱いが複雑となる。これは磁界が種々異なる物質(媒質)で構成されているためで、このような不都合を解消するため、媒質の磁気的性質を表す透磁率(実数値)という量を導入することで対応する。つまり、磁力線の透磁率倍という『磁束』という指力線を考えると、この線はどの媒質中でも同じ値となるので、磁束は磁界中で閉じた指力線となり、磁界の取り扱いが容易となる。
磁力線密度が磁界の強さH〔A/m〕に等しいので、透磁率をμとすれば、磁束Φ〔Wb〕の線密度(磁束密度)Bとの間には、
という関係が成立している。
したがって、これまでに扱った媒質が単一な直線電流や円形電流の場合の磁力線分布は磁束分布と考えて扱ってよい。なお、磁石の磁束分布の例を第7図に示す。この場合も磁石外では第1図に示す磁力線分布が磁束分布と考えればよいことになる。
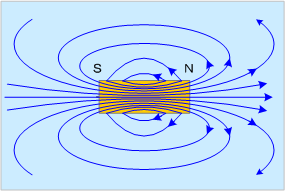
第7図 磁石がつくる磁界の磁束分布
(5)強力な電磁気をつくる仕組み
第8図(a)のように、コイルの中に材料Bを挿入してみる。この材料が強磁性体と呼ばれている材料の場合は磁束が格段に増加する。その仕組みは、コイルに電流を流すと、その磁界により水色の磁束Φ0ができる。ここで、材料中の赤点線部に注目すると、
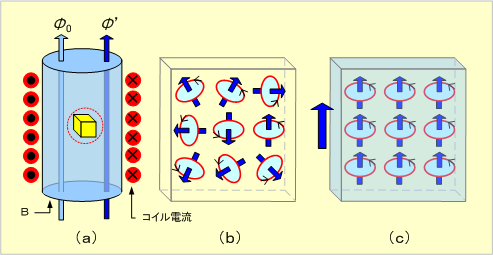
第8図 強磁性体を入れたコイルがつくる磁界
磁界のない場合は内部の分子・原子レベルでは電子のスピン運動等により円形電流が形成されているため、個々に磁性をもってはいるが、これらは互いに勝手な方向を向いているため、全体としては外部に磁性は現れない(同図(b))。しかし、コイルに電流を流すことによりできた磁界によって各々の円形電流は第9図に示すように磁界の方向に力を受け、その方向に向きを変えるため、第8図(c)のような配列となり、材料中には第8図(a)に示す磁束Φ´が加わることになり、磁性が強くなる(磁束が増加する)。
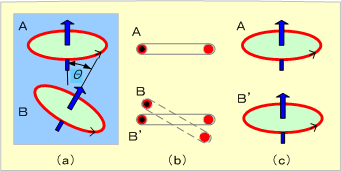
第9図 円形電流間に働く力
第10図 磁石をいろいろな方向から運動させてみる
第10図のように、コイルの両端に検流計Gを接続し、
① 青色部がN極の磁石をA1からA2まで一定速度で運動させると、Gの針が振れはじめ、その振れはA2に近づくにつれて次第に大きくなり、最大目盛(K)に達する(A1脇の再生ボタン>をマウスでクリックすると、磁石の運動と針の振れの様子が観察できる)。続いて、
② 磁石をBコースで①と同じ速度で運動させると、Gの針の振れは、①と同じように変化するが、振れの大きさは①より全ての範囲で若干小さくなり、Kの約70%に至る(B1脇の>ボタンをマウスでクリックすると、その様子が観察できる)。さらに、
③ 磁石をCコースについて、①と同じ速度で運動させてみると、Gの針は全ての区間で振れない(C1脇の>ボタンをマウスでクリックすると、その様子が観察できる)。
このような一連の現象がなぜ起こるのか。ファラデーは
『鎖交磁束が時間とともに変化するため回路に起電力が発生する結果である』
『発生する起電力の大きさは鎖交磁束の時間的変化率に比例する』
ことを突き止めた。
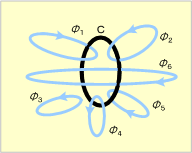
第11図 鎖交磁束
第12図 鎖交磁束の増減
磁束とコイルC(回路)とが鎖と鎖が繋がるような関係にあることを鎖交といい、このときの磁束を鎖交磁束という。第11図ではΦ1とΦ2が鎖交磁束である。第10図①を例にあげると、磁石がコイルに近づくにつれて次第に鎖交磁束が増加して行く。これに対し、②ではコイルに向かう磁束が斜めの方向からとなるため、①に比べ鎖交磁束の量そのものが減少し、①より針の振れが小さくなる。③の方向から磁石を運動させた場合は、コイルと鎖交する磁束はできないため、Gの針は振れないことになるわけである。これら鎖交磁束の変化の様子は第12図でよく観察して頂きたい。次に、
第13図 磁石の運動速度を変化してみる
④ 第13図のように、①の例で見ると、磁石の速度を①の0.5倍にしてみると、針の振れは元の速度の場合の0.5倍となる。(2個の>ボタンを押して各々の場合を観察する)。次に、
第14図 コイルの巻数を変えてみる
⑤ 第14図のように、①の場合で、コイルの巻数を5から3に変えてみると、針の振れは元の0.6倍となる。この結果、
『発生する起電力は「鎖交磁束Φ×コイルの巻数N」の時間的変化率に比例する』
ことがわかる。次に、
第15図 電磁気による実験
⑥ 第15図のように、磁石を「電流が流れているコイル」に置き替えて、①の方向で実験すると、Gの針は①の場合と同じような振れを示す(図中の上と中の>ボタンを押して観察する)。続いて、
⑦ ⑥でコイルに流す電流を半分に減らして実験すると、針の振れも半減する(図中の下の>ボタンを押して観察する)。次に、
第16図 磁石の運動方向を逆にしてみる
⑧ 第16図のように、検流計を正負の目盛をもつものに替え、磁石をA1からA2まで一定速度で運動させると、Gはプラスに振れ、次に、A2からA1へ一定速度で運動させると、Gはマイナスに振れる(左右の>ボタンを押して観察する)。今度は、
第17図 電磁気で運動の方向を変えてみる
⑨ 第17図のように磁石を「電流が流れているコイル」に置き替えて、⑧と同様な実験をすると、⑧と同じような結果が得られる(左右の>ボタンを押して観察する)。
この結果から、磁束発生体の運動方向を変えると、鎖交磁束の増加か減少が起こり、その増減によって起電力の方向が変化することがわかる。起電力方向の見定め方は、『磁束は時間的に変化することを嫌う』という性質を念頭に、第18図の右手親指の法則か、レンツの法則で調べればよい。次に、
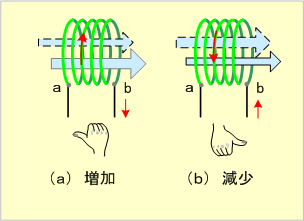
第18図 起電力の方向は、どのようにして知るか
第19図 電磁気でいろいろな電流変化を与えてみる
⑩ ⑦は「磁束は電流に比例する」ことから当然の結果である。とすれば、第19図のように、コイルPを固定したままで、コイルへ流す電流iをイ ロ ハ ニのように変えてみると、Gの針の振れは、
(1)イでは、0T区間で常に一定値(K/2)を指示する。
(2)ロの場合は、0T区間で常にK/4(イの1/2)を指示する。
(3)ハの場合は、0T区間で常に針は振れない。
(4)ニの場合は、0T1区間ではK、T1T2区間では0、T2T区間では−K/2、をそれぞれ指示する(各々の>ボタンを押して観察する)。
以上の内容から、この現象は次のように要約できる。
(1)鎖交磁束が時間と共に変化すると、コイル(回路)に起電力が発生する。この現象を電磁誘導現象という。このとき発生する起電力を誘導起電力といい、誘導起電力によって回路に流れる電流を誘導電流という。
(2)誘導起電力は、磁束鎖交数(巻数×鎖交磁束)の時間的変化に比例する。
・・・ファラデーの法則
(3)誘導起電力は、鎖交磁束の変化を妨げる方向に発生する。
・・・・・・・・レンツの法則など
(1)基礎となる用語と事項を理解する。
磁界、電流の磁気作用、右ねじの法則、右手親指の法則、磁束、鎖交、鎖交磁束、磁束鎖交数など。
(2)電流のつくる磁界(電磁気)の代表的なパターンを知る。(直線電流、円形電流、円筒状コイルなど)について、その磁界を磁束で表すことを理解し、その概略を図示できること。
(3)電磁誘導現象。誘導起電力の大きさと方向の定性的な理解。
(ファラデーの法則、レンツの法則、右ねじの法則、右手親指の法則)
(4)電流の流れるところ全てのところに電磁誘導現象が発生する。
(5)電気を発生させる基となる原理である。
(6)電線を接続しなくても電気が送れる。離れた場所へ電気を送る。
(7)いま注目されている二つの「I」は、「IT」と「IH」。
