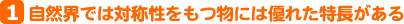我々の作る機械の中でも、特に運動を目的にする乗り物などは、船でも自動車でも力学的バランスをとるため、左右対称に設計するのが建前になっている。もし左右対称でないと右か左に傾く癖がでてしまうから、運転が難しくなる。


電気回路を考える場合、電流の流れる回路が対称性をもっていると、対称性のない回路よりもバランスがとれていることになり、安定状態にあるから解きやすくなる。本講では、対称性のある電気回路の解き方を、やさしいものから幾つかの例題をもとに説明する。
Update Required To play the media you will need to either update your browser to a recent version or update your Flash plugin.
※テキスト中の図はクリックすると大きく表示されます
はじめに対称性ということを広く自然界で考えてみると、それぞれ優れた特長があることが分かる。例えば、ほとんどすべての動物の体形は左右対称にできているが、これは動物が運動や行動する際に、力学的バランスをとるうえで大きな効果をもたらしてくれている。鳥や昆虫にしても、もし体形が左右対称でないと安定して飛ぶことは難しくなってしまう。逆に、草や木が対称になっていないのは運動しないからだともいえる。
我々の作る機械の中でも、特に運動を目的にする乗り物などは、船でも自動車でも力学的バランスをとるため、左右対称に設計するのが建前になっている。もし左右対称でないと右か左に傾く癖がでてしまうから、運転が難しくなる。
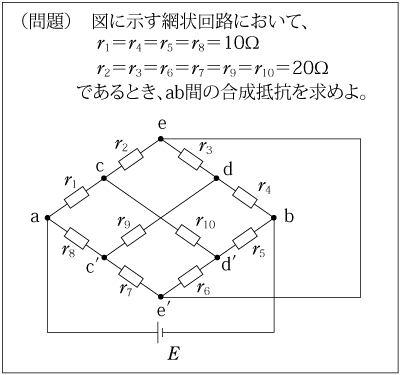
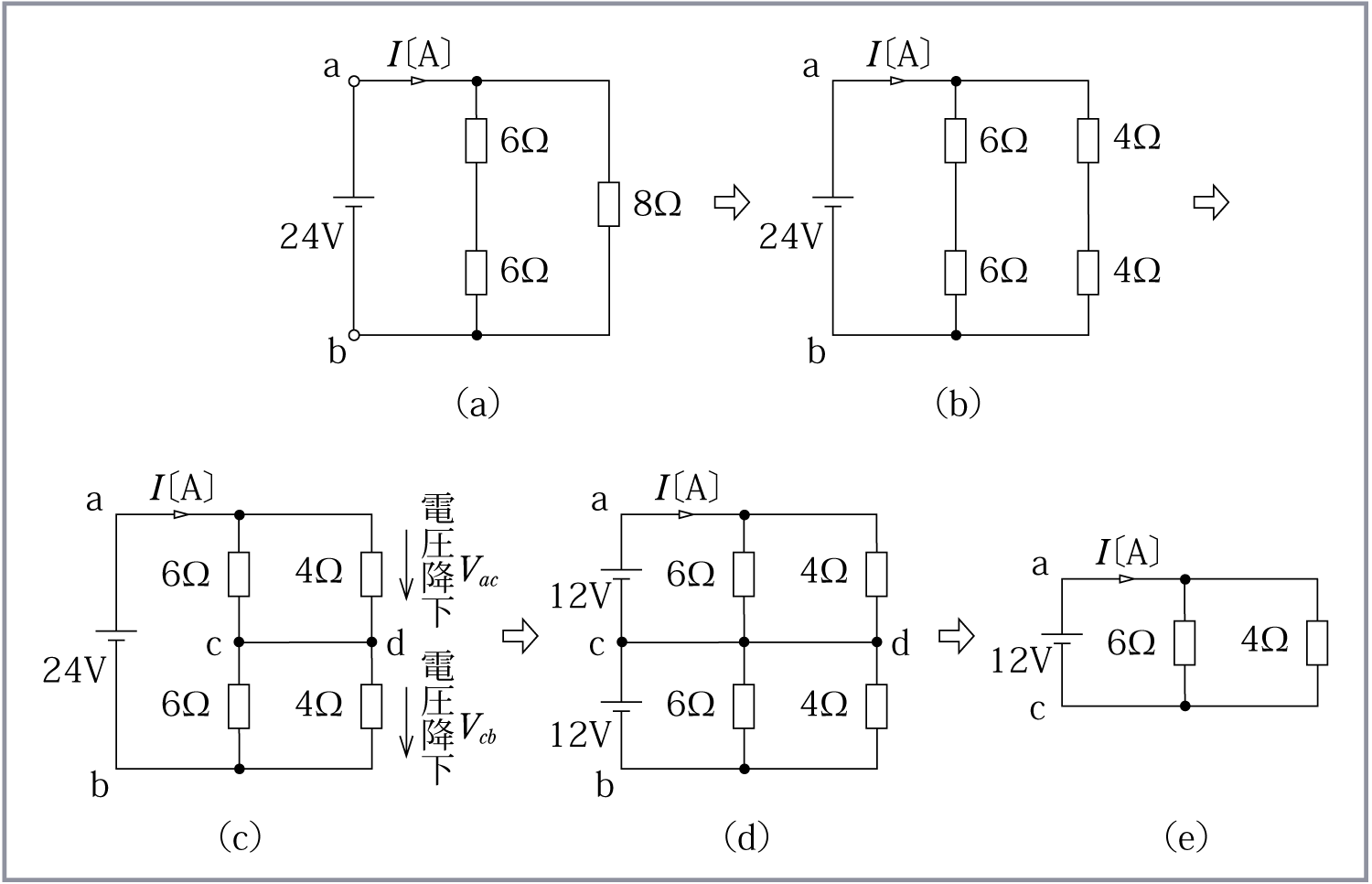
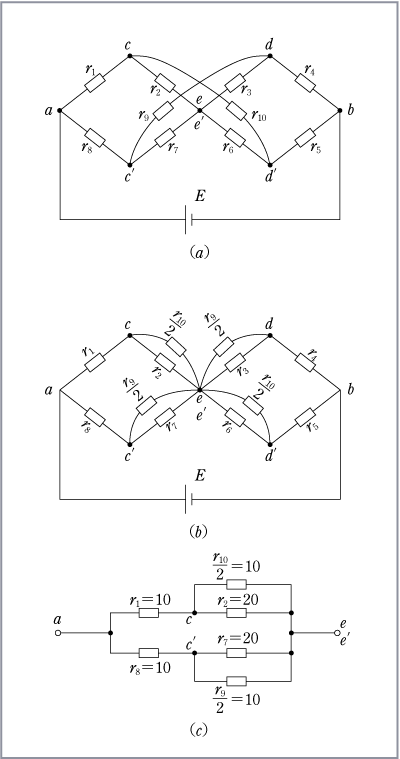
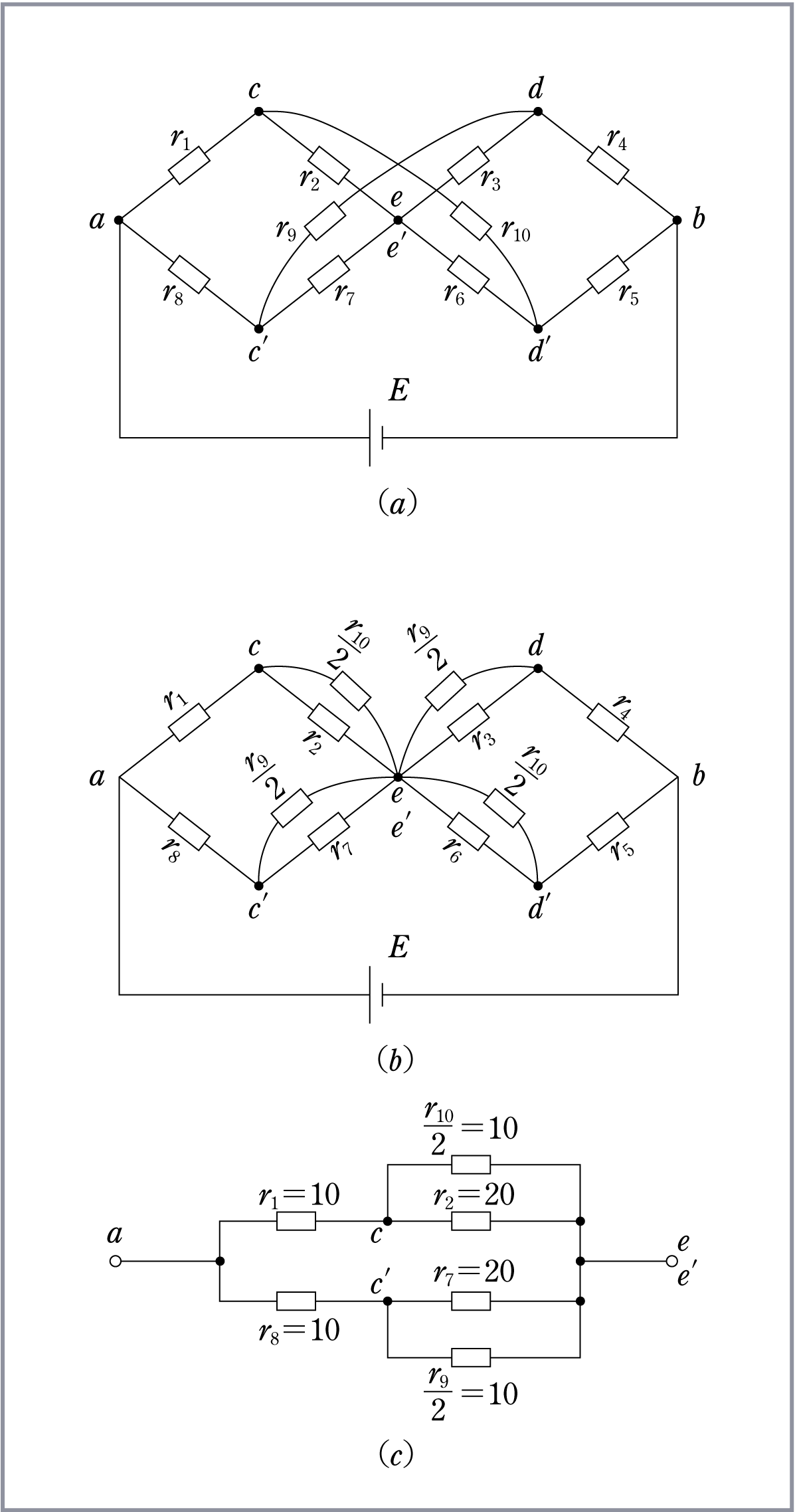
例えば、第1図に示すような複雑な回路の合成抵抗を求めようとすると、一見しただけではどう扱ってよいか分かりにくい印象を受けるが、この回路の対称性に着目すると、比較的容易に解答を導くことができる。この場合、解法のポイントは回路のどの地点でバランスがとれているかを発見することにある。具体的にいえば、対称性のある回路の中で同じ電位の地点がどこにできているかを探し、見付けたら、そこが対称性の中心と考えて回路を等分に分割することである。この作業によって回路は簡単化され、処理しやすくなる。
では手始めに、対称性のある簡単な回路の解き方、考え方を、やさしいものから幾つかの例題をもとに説明していき、最後に第1図の回路を解いてみる。
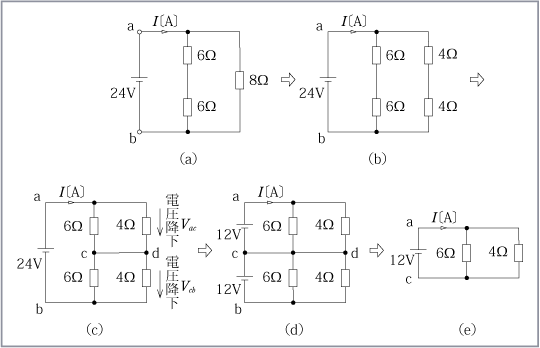
次に第2図 (c) のように、この回路の同じ対称性回路を分割する点 cd 間は電位が等しいから、直接接続しても回路に何の影響も与えない。(ホイートストンブリッジの平衡条件が成立している)対称性のある回路というものは、同電位の点がこういうところにできていることに注目してほしい。この第2図 (c) で電圧降下VacとVbcは等しいから、更に第2図 (d) のように電源電圧 24Vを12Vずつに分けて cd に接続しても、回路の電流Iは変わらない。そこで、回路を分割した第2図 (e) は簡単であるから、電流Iと合成抵抗は容易に求められる。すなわち、
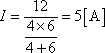
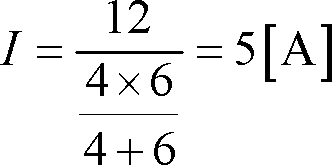 となる。結局、最初の回路の合成抵抗Rabは第2図 (e) の6Ωと4Ωの並列抵抗が2組直列にあるので、
となる。結局、最初の回路の合成抵抗Rabは第2図 (e) の6Ωと4Ωの並列抵抗が2組直列にあるので、 ① 直列接続でまとめる場合
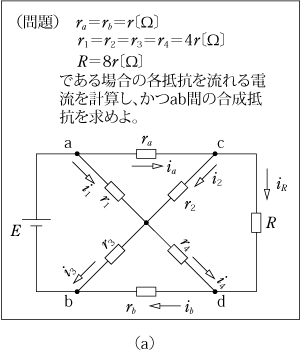
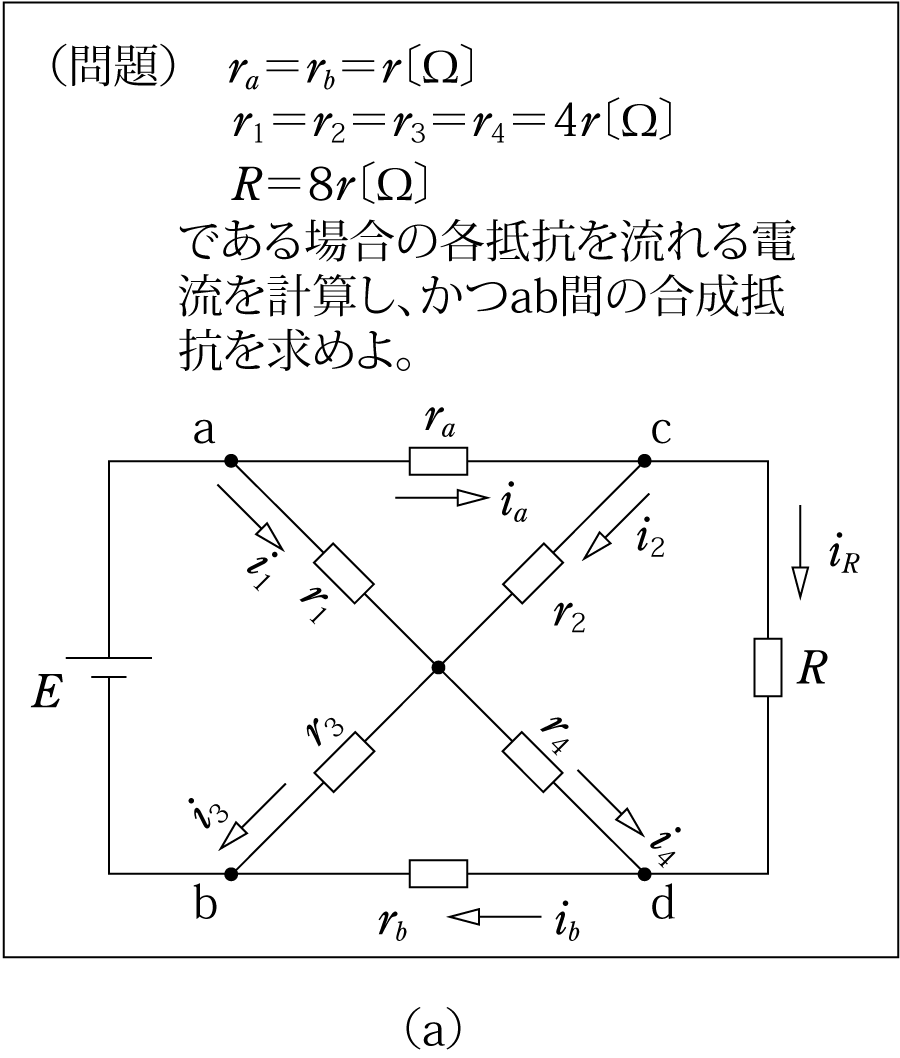
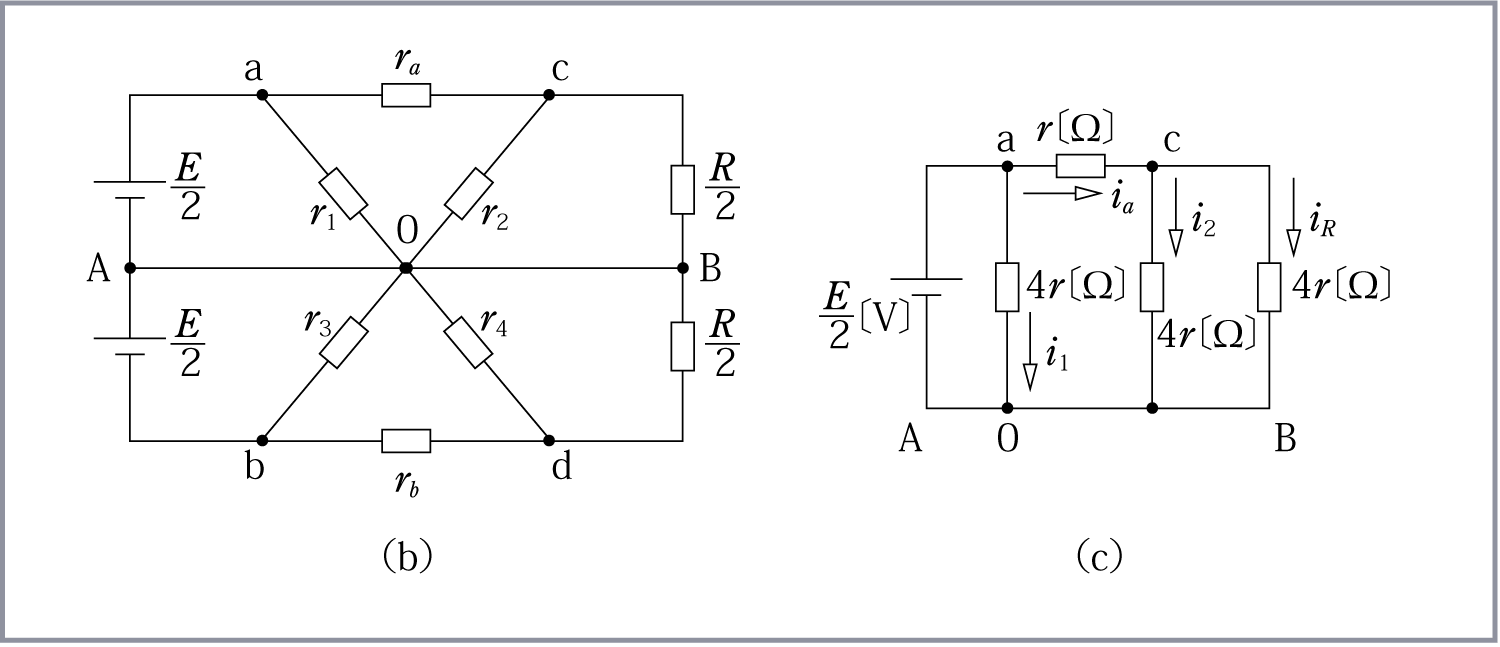
第2図の問題と同じ考え方で、第3図 (a) の問題を解いてみよう。(考え方)
抵抗Rを2分割すると第3図 (b) のように、上下で対称な回路になることが分かる。上の回路集団は第3図 (c) のようになるから、まずこの合成抵抗RaO を求めると、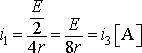
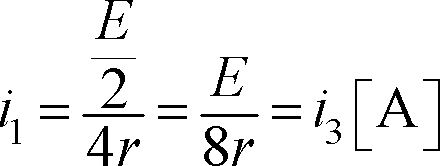
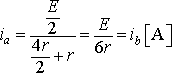
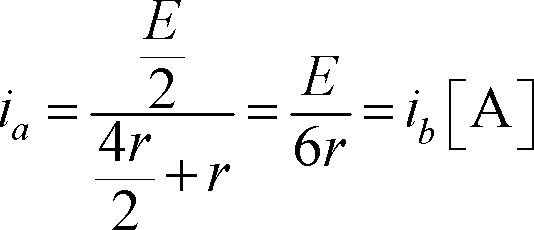
② 並列接続でまとめる場合
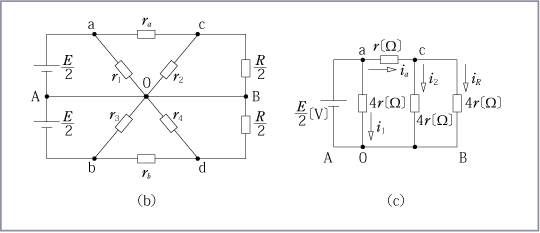
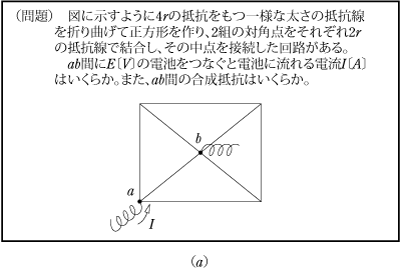
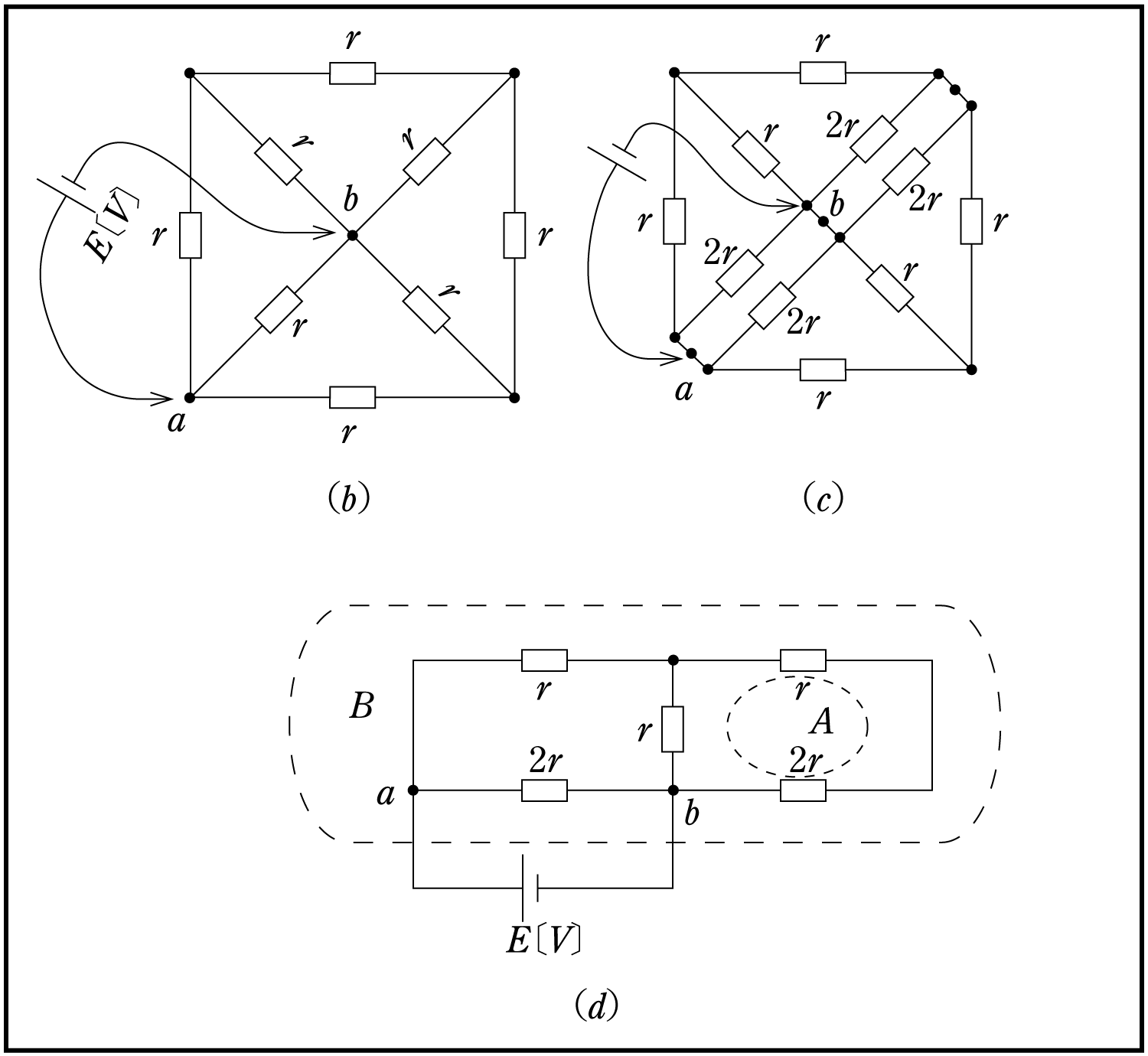
第4図(a)に示す抵抗線を折り曲げた回路の問題を解いてみよう。(考え方)
抵抗回路に置き換えると、第4図 (b) のようになる。着眼点は電源側から考えるとよい。電源のつながっている対角線の抵抗を二つに割って(並列)みると、第4図 (c) のように左上の三角部分と右下の三角部分に同じ回路集団ができることが分かる。そうすると1個の回路集団は第4図 (d) のようになることが分かる。第4図 (d) の点線で囲まれたA部分の抵抗RAは、
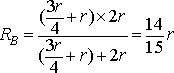
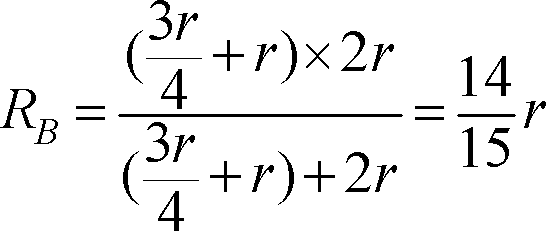
~終わり~
■ぜひアンケートにご協力下さい■