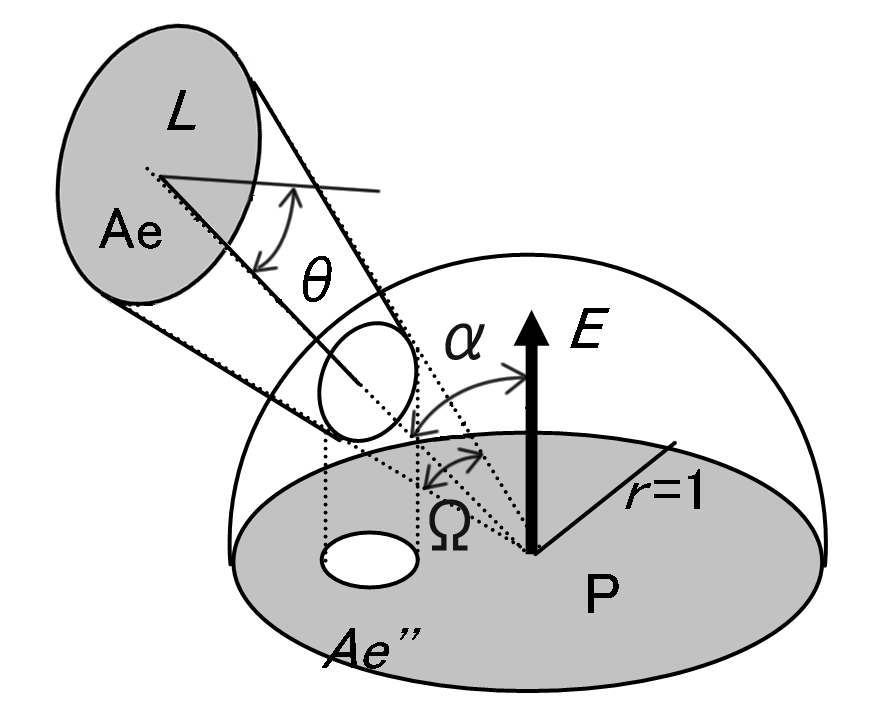
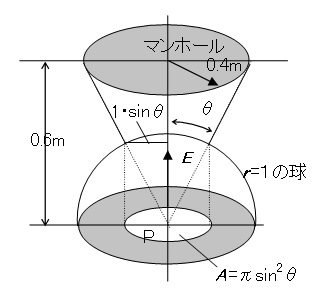
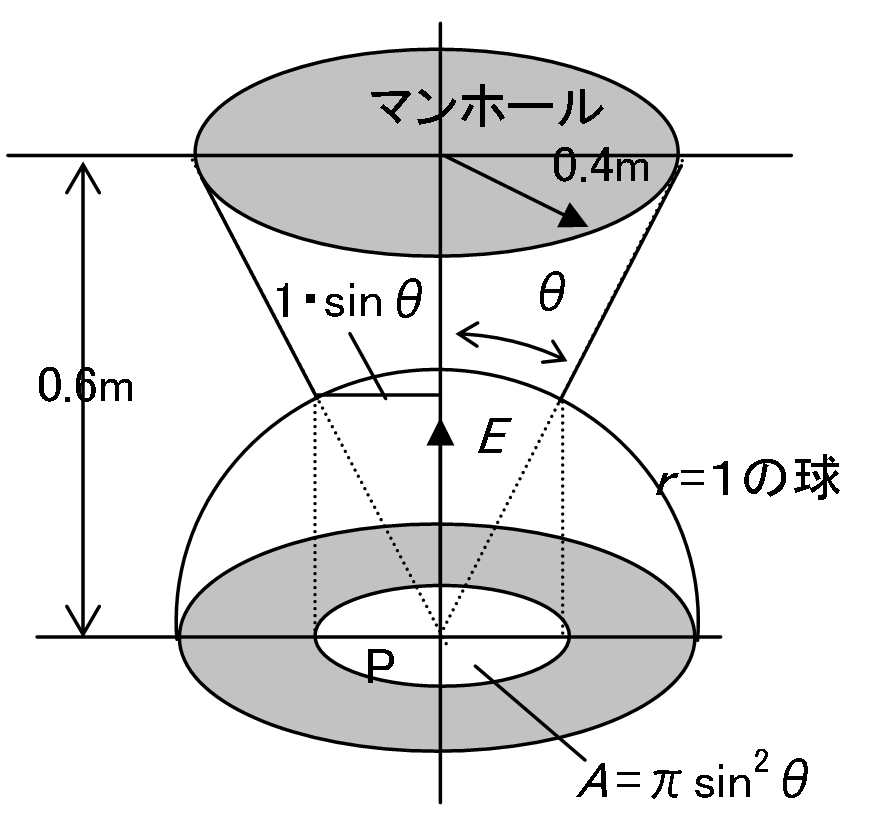
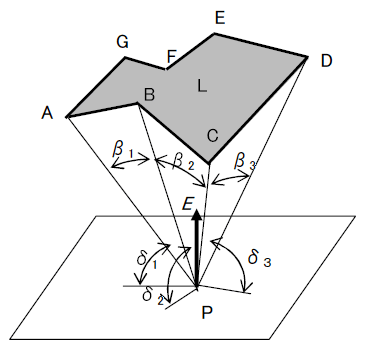
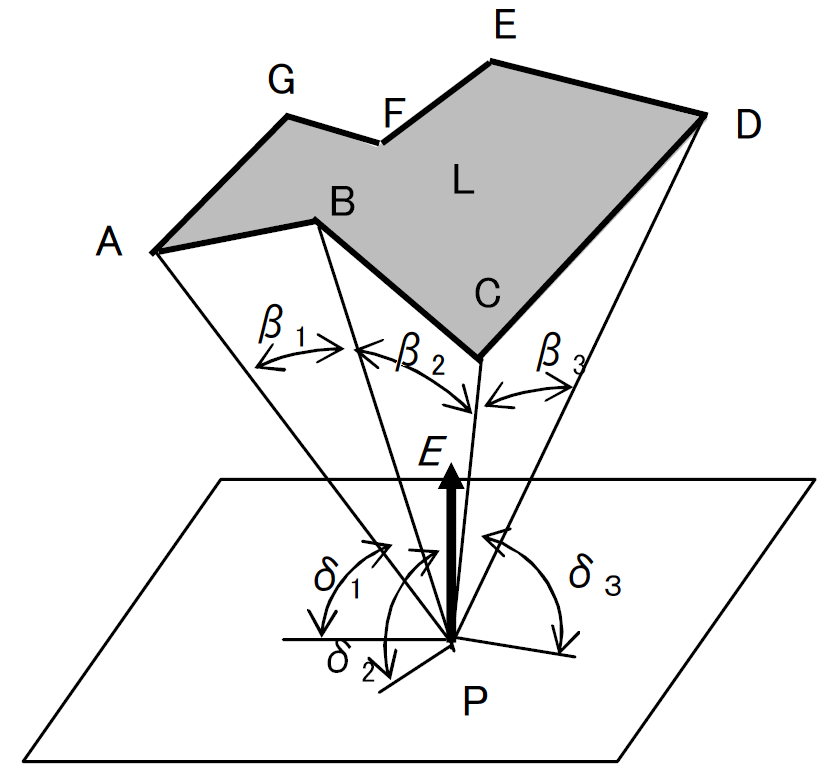
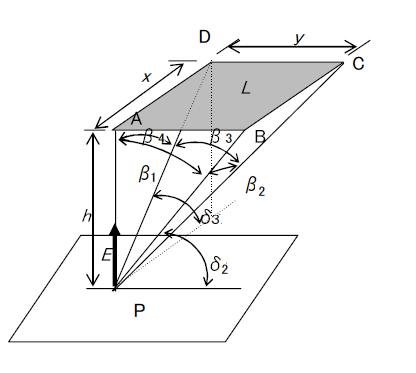
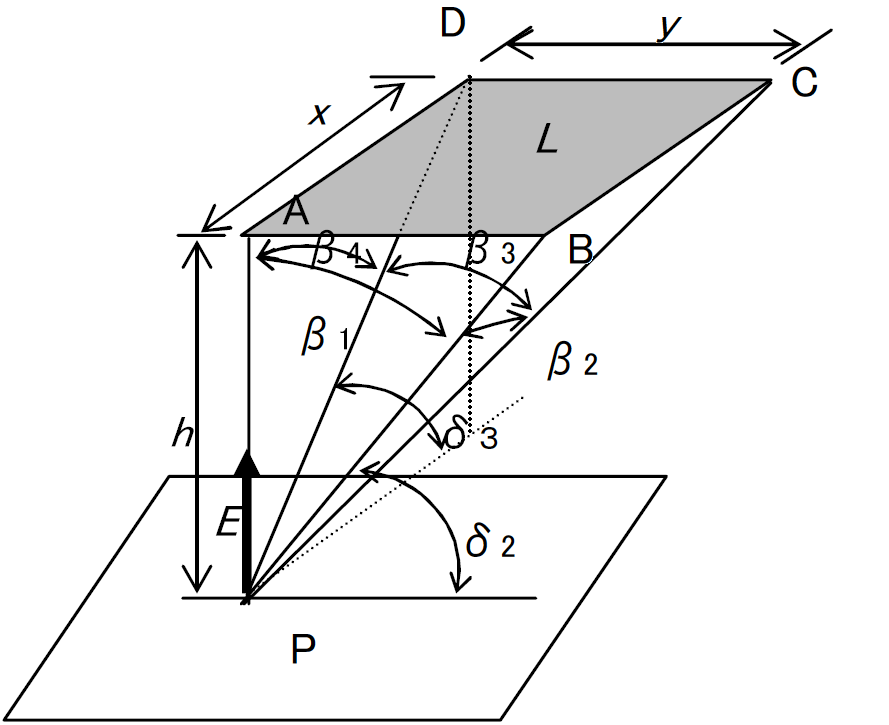
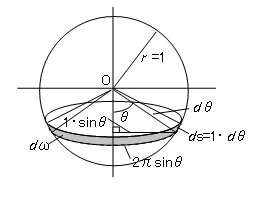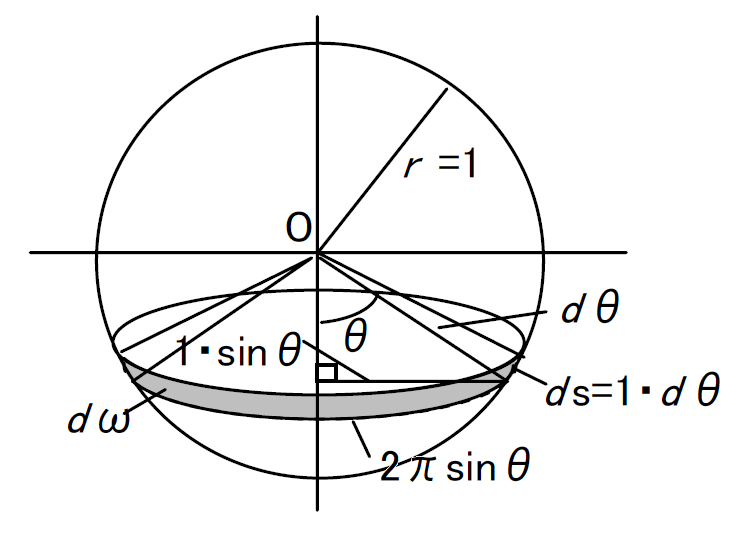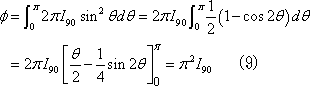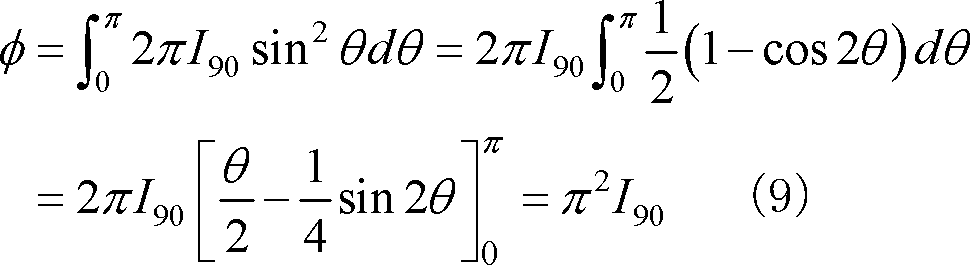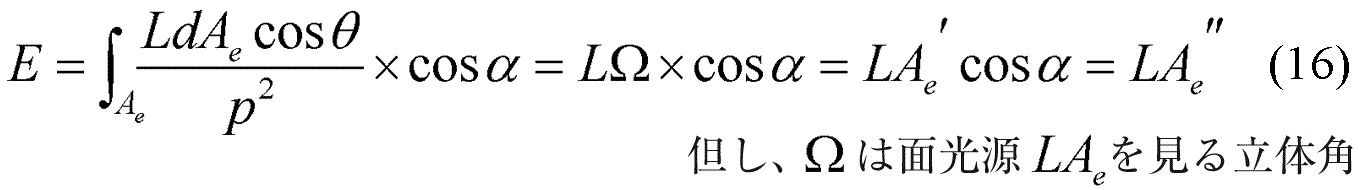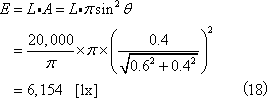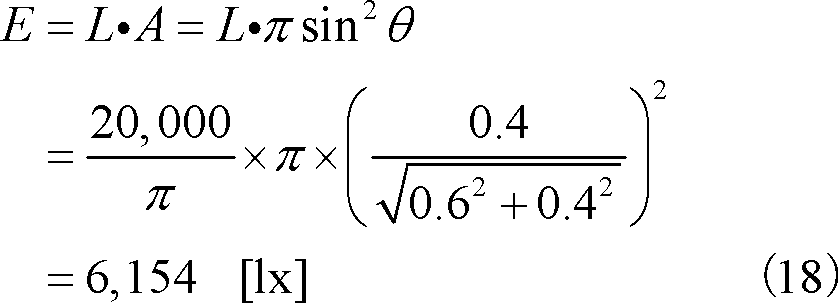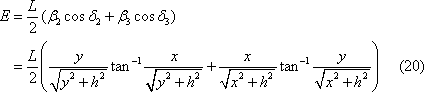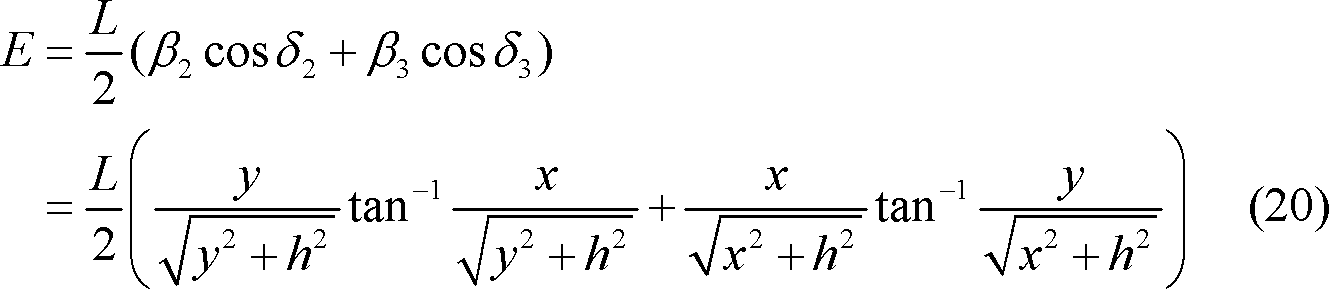1.1 放射束
放射とは、エネルギーが電磁波として空間に放出される現象です。電磁波のなかで、波長が380〜780nmの範囲の放射は、人の目に入ったとき光として明るさを感じさせます。このように目に見える光を可視光線と呼びます。
放射束は、ある面を単位時間に通過する放射エネルギーの量であり、その単位はワット[W]です。この放射束は人の目に無関係な物理量です。
1.2 光束[lm(ルーメン)]
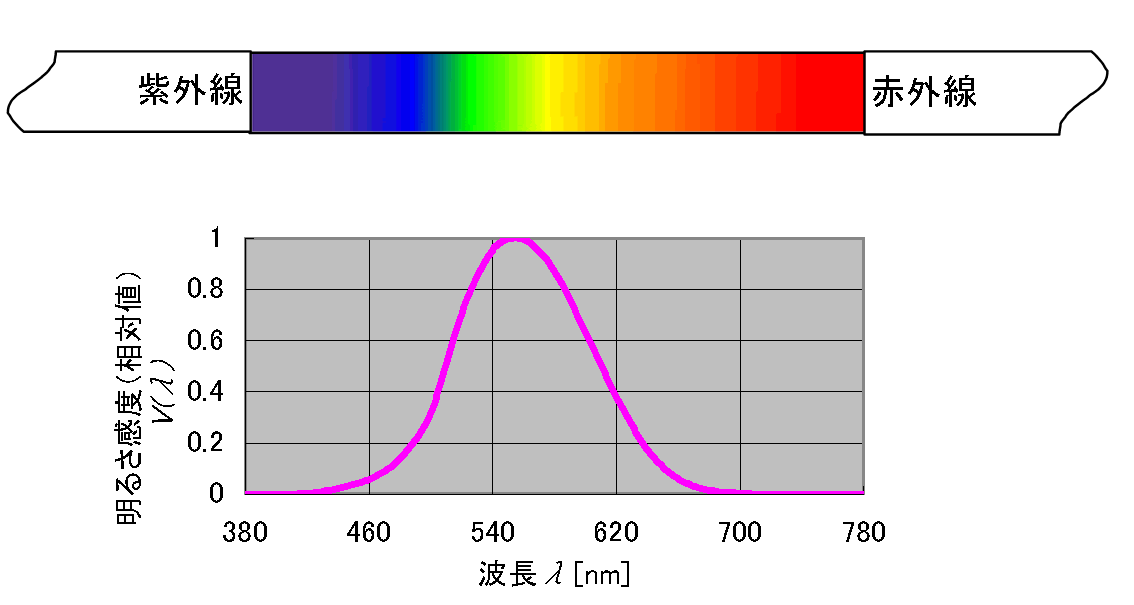
測光量である光の量は、可視光線を目の感度のフィルタ(視感度)を通して見た量で、このフィルタの特性曲線
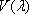
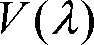 は第1図のように表されます。これは、国際的に取り決められたものでCIE標準比視感度と呼ばれ、波長555nmの黄緑の光に対して最大感度を1とし、同等のエネルギーをもつ他の電磁波の明るさ感を比較値(相対値)で表しています。
は第1図のように表されます。これは、国際的に取り決められたものでCIE標準比視感度と呼ばれ、波長555nmの黄緑の光に対して最大感度を1とし、同等のエネルギーをもつ他の電磁波の明るさ感を比較値(相対値)で表しています。
光束
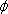
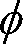 は、上記の比視感度
は、上記の比視感度
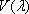
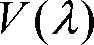 を用いて次式で表されます。
を用いて次式で表されます。
ここに、光束 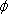
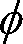 の単位:ルーメン[lm]、
の単位:ルーメン[lm]、 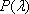
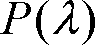 :分光放射束(波長
:分光放射束(波長
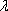
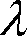 における放射束の単位波長幅当りのパワー)[W/nm]、
における放射束の単位波長幅当りのパワー)[W/nm]、 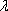
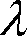 :波長[nm]、
:波長[nm]、 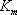
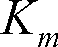 :視感度が最大になる波長における放射束と光束の換算係数で683 lm/Wです。
:視感度が最大になる波長における放射束と光束の換算係数で683 lm/Wです。
このように、光束は人の目という計測器を通して放射束を測った量であり、以下の測光量の基本です。
1.3 光度[cd(カンデラ)]
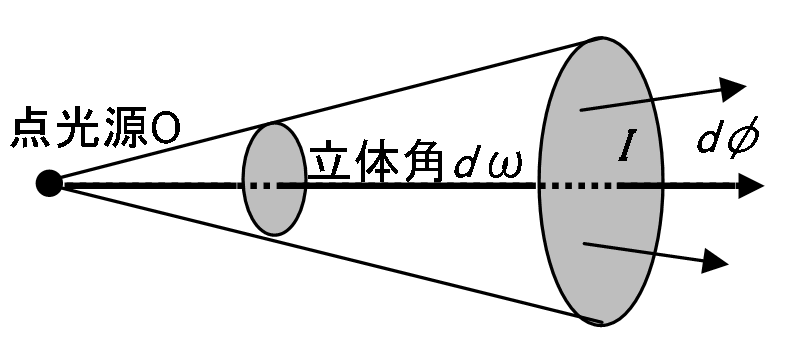
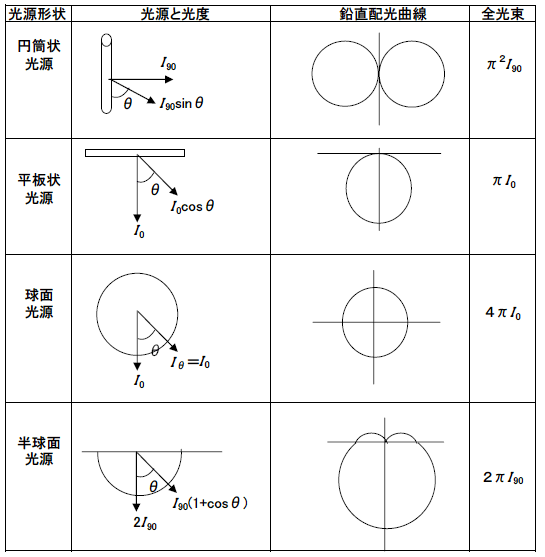
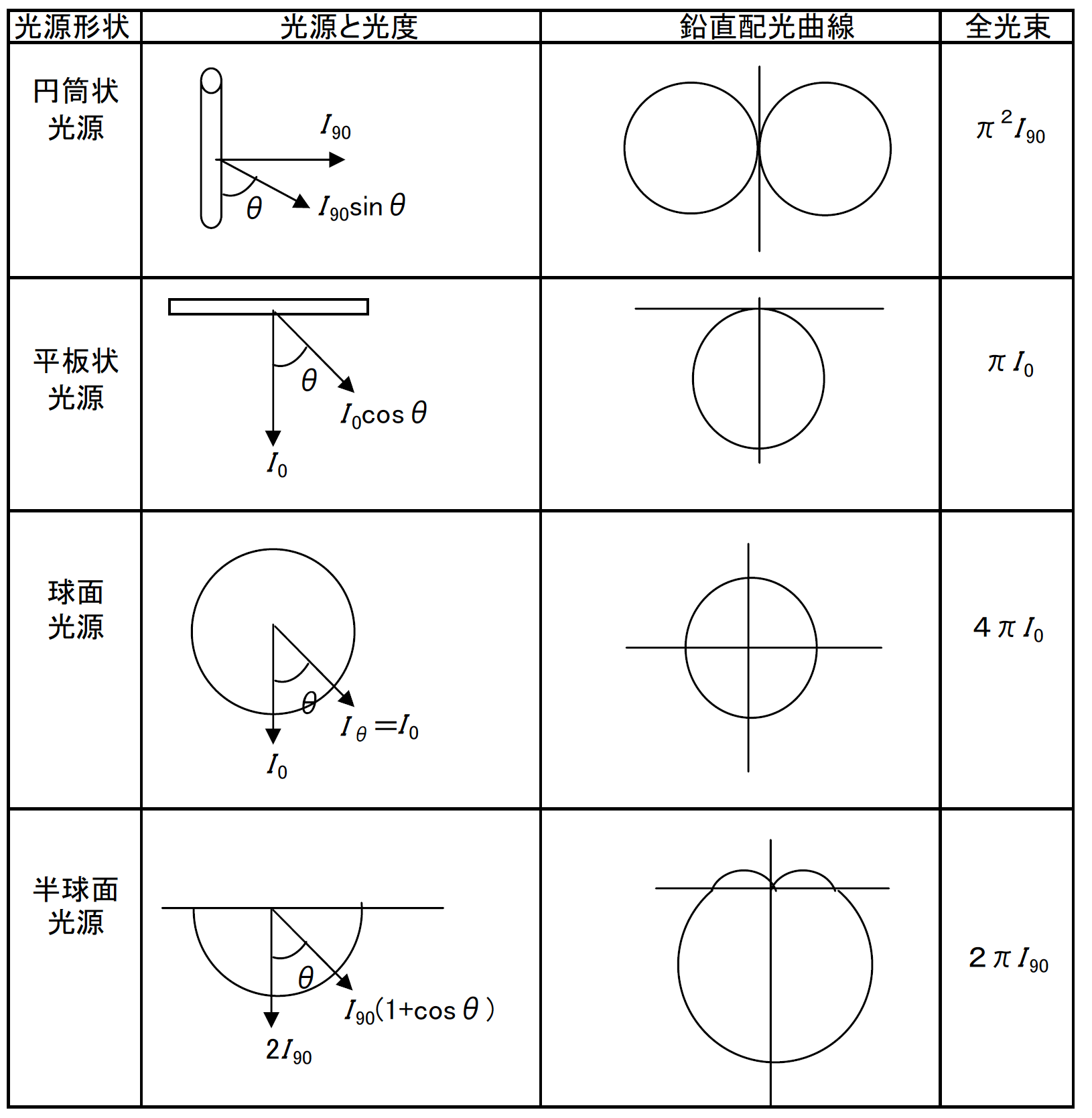
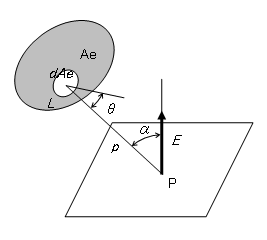
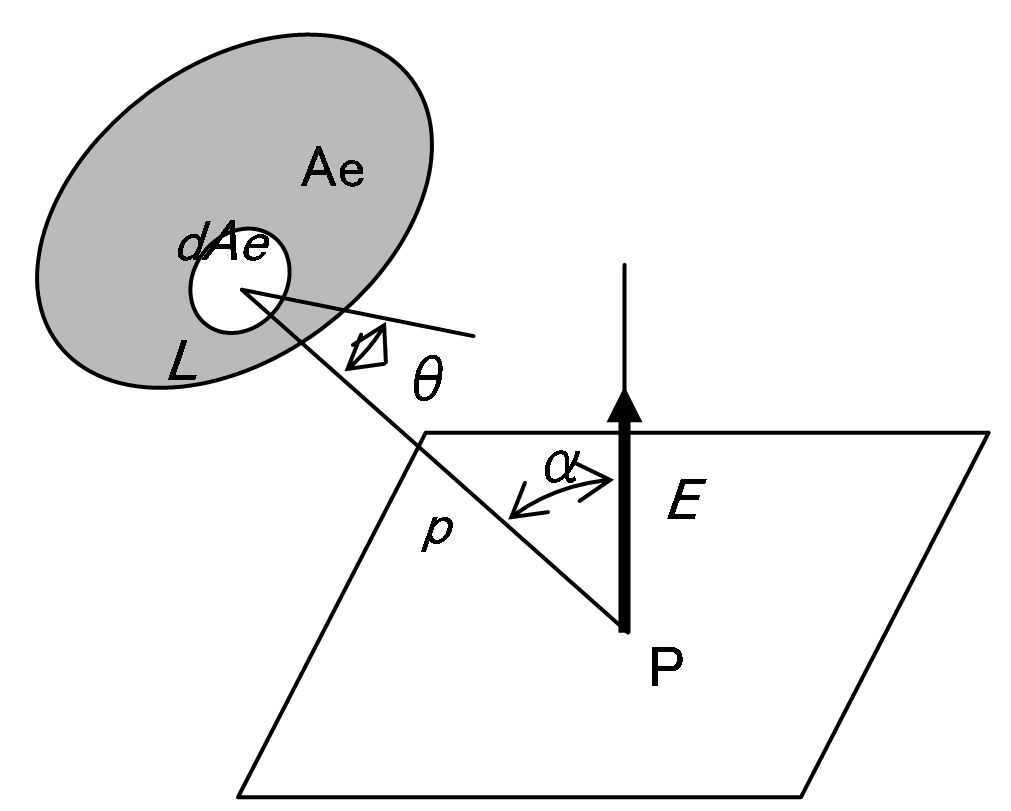
ある方向の単位立体角内に発散される光束、すなわち、光束の立体角密度を光度といい、単位はカンデラ[cd]です。
光度を
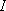
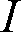 [cd]、光束を
[cd]、光束を
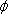
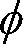 [lm]、立体角を
[lm]、立体角を
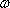
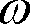 [sr]とすれば、光度
[sr]とすれば、光度
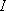
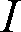 は次のように表されます。
は次のように表されます。
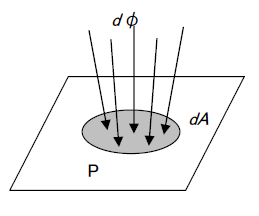
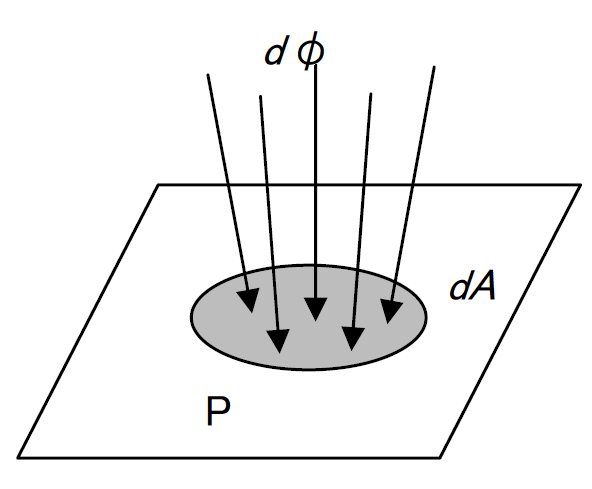
1.4 照度[lx(ルクス)またはlm/m2]
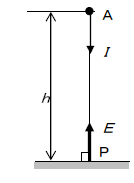
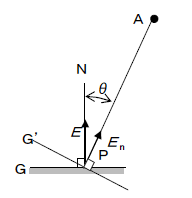
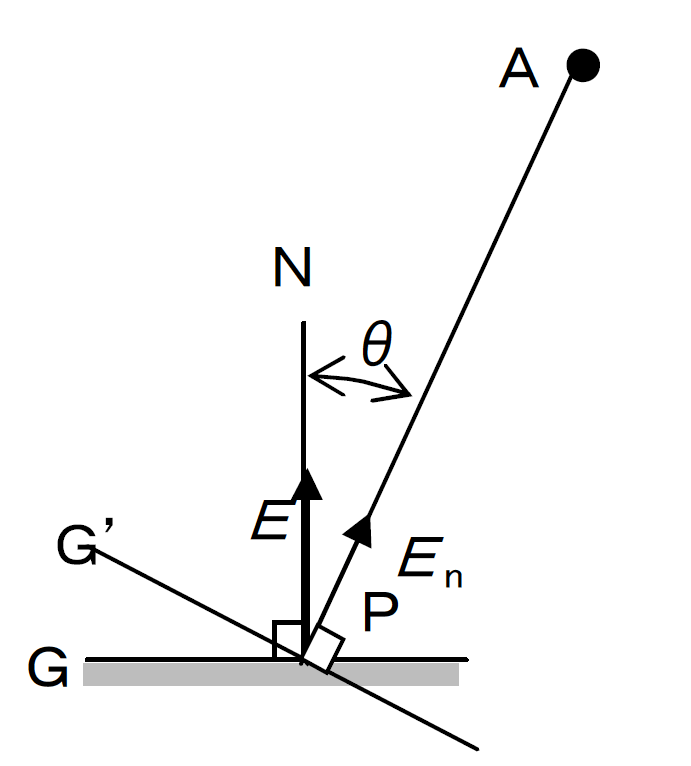
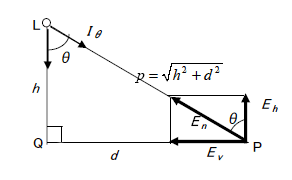
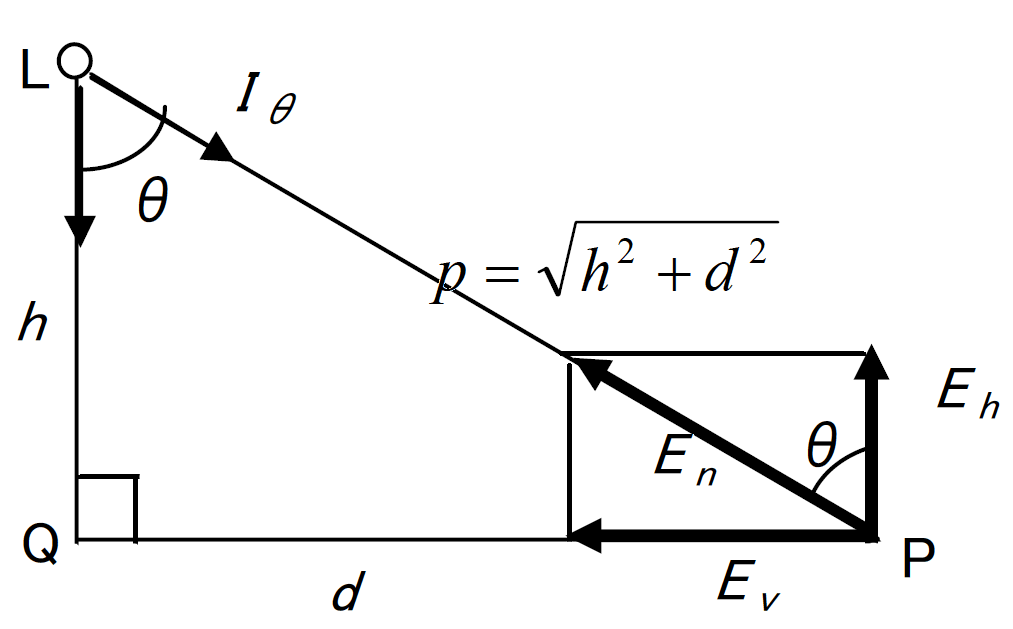
光源によって照らされている場所の明るさの程度を表し、ある面に入射する光束をその面の面積で割った値です。
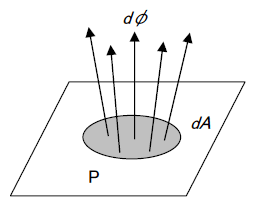
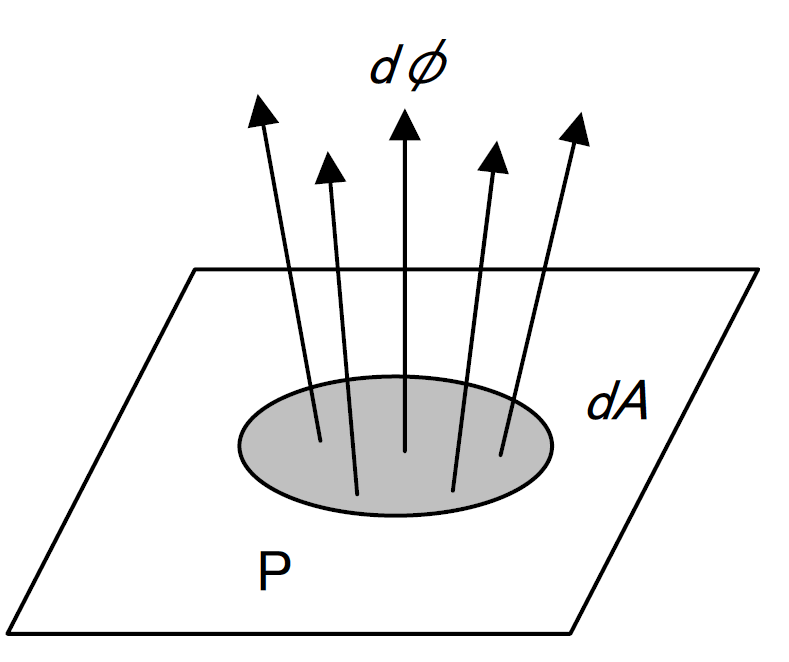
ある面Pへの入射光束
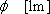
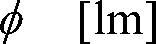 、入射面積を
、入射面積を
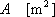
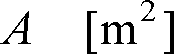 とすれば照度
とすれば照度
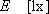
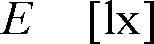 は
は
です。
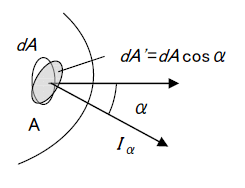
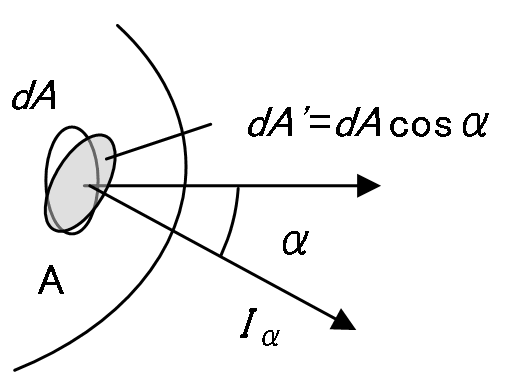
1.5 輝度[cd/m2]
光っている面や照らされている面の明るさを表す量が輝度です。光源や被照面からの光度を、その方向へ見掛けの面積で割った値です。すなわち、光度の面積密度であり、第4図のように輝度
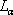
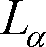 は
は
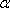
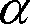 方向の光度
方向の光度
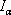
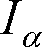 [cd]をその方向から見た見掛けの面積
[cd]をその方向から見た見掛けの面積
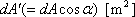
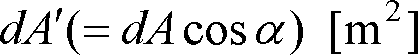 で割った値で表されます。
で割った値で表されます。
蛍光ランプは、広い面積から光が出ているため輝度が低いですが、白熱電球は面積が非常に小さいフィラメントから光が出ているために輝度が高いです。
1.6 光束発散度[lm/m2]
発光面(反射面、透過面を含む)の微小面積
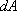
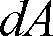 を通りそこから発散する光束を
を通りそこから発散する光束を
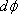
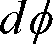 とするとき光束発散度
とするとき光束発散度
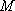
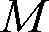 は
は
です。
反射面、透過面の光束発散度は、反射率
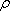
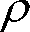 、透過率
、透過率

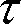 と照度
と照度
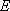
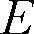 との間に次の関係があります。
との間に次の関係があります。
また、どの方向から見ても輝度が等しい表面を完全拡散といいます。完全拡散では、輝度
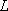
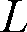 と次の関係があります。
と次の関係があります。