電気回路の電圧、電流、などの計算は、回路の複雑さや計算目的から判断して、ご質問のように、キルヒフホッフの法則、重ねの理、テブナンの理、などを臨機応変に活用して行っています。実務においては、これらの計算方法や違い・特徴等を分かりやすい方法でしっか
り身に付けておき、何時でも間違い無く使えるようになることが大事になります。
以上を念頭に、ここでは極力同じ電気回路を用いてそれぞれの方法で計算し、その上で特徴や使用面の留意事項を述べることにします。
未知数(ここでは、I1,I2,I3の3個)分の方程式を立て、直接解く最も基本的な計算方法です。未知数が多いと解くのが困難になります。
② 電気回路例
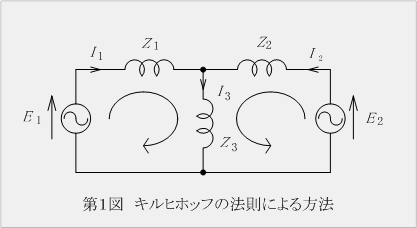
(「閉回路の電源電圧の総和=電圧降下の総和」と「分岐点の電流の総和=ゼロ」)
E1=Z1I1+Z3I3 ------- (1)
E2=Z2I2+Z3I3 ------- (2)
I1+I2-I3=0 ------- (3)
④ 各部の電流の大きさ(上記の方程式を解く。ここでは結果のみを示します。)
① 解き方、特徴
各電源が単独にあるときの各部の電圧・電流を求め、それらを加え合わせる方法。
ここでは電源が二つなので、二つの回路に分けて計算することになる。
一見、面倒に見えるが、簡単な数式の集まりなので簡単に解ける場合が多い。
② 電気回路例
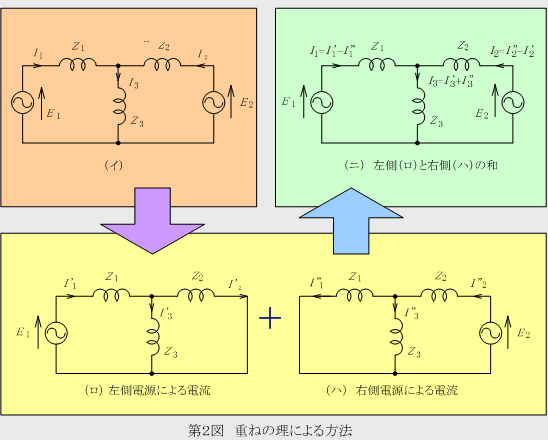
③ 各回路の式を解く(第2図の(ロ)や(ハ)の電流から(ニ)の電流を求める )
(ロ)の回路の電流
![]() ------ (7)
------ (7)
![]() ------(8)
------(8)
![]() ------(9)
------(9)
但し、Δ=Z1Z2+Z2Z3+Z3Z1
(ハ)の回路の電流
![]() ------(10)
------(10)
![]() ------(11)
------(11)
![]() ------(12)
------(12)
但し、Δ=Z1Z2+Z2Z3+Z3Z1
(ニ)の回路の電流 ( (ニ)=(ロ)+(ハ) として求める )
![]() ------(13)
------(13)
![]() ------(14)
------(14)
![]() ------(15)
------(15)
但し、Δ=Z1Z2+Z2Z3+Z3Z1
求める各回路の電流(I1,I2,I3)は、(13),(14),(15)式となり、キルヒホッフの法則により求めた各回路の電流は(4),(5),(6)式と同じになる。
① 解き方、特徴
変化前(ここではZ3が無いとき)の電流(第3図(ロ)のIL)と変化分の電流
(第3図(ハ)の各回路の電流)を求め、それらを加え合わせる方法。
一般に、テブナンの理は、(ハ)のZ3を流れる電流(ここではI'3)を指していますが、図のように変化分と見ることができる。
(第3図(イ)は、Z3が新に接続されることを念頭においた図です。キルヒホッフの法則による方法や重ねの理による方法と極力同じ電気回路を用いて説明するためです。少し無理をしていますが、理解していただけると思います。)
② 電気回路
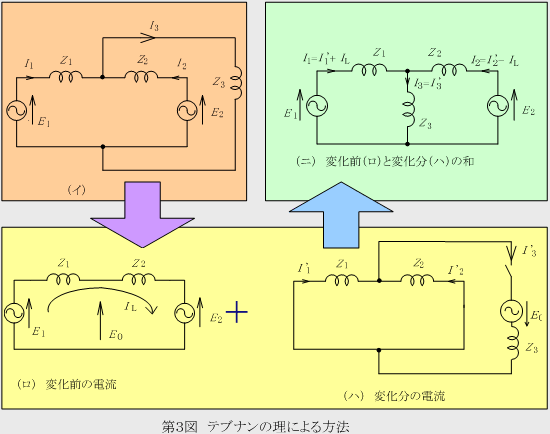
③ 各回路の式を解く
(ロ)変化前の電流(IL)、電圧(E0)
IL、E0は、簡単な回路であり、(16),(17)式のようになる。
![]() ------ (16)
------ (16)
![]() ------ (17)
------ (17)
(ハ)変化分の電流(I'3,I'1,I'2 )
I'3は、電圧E0、インピーダンス(Z0+Z3)から、(18)式のようになる。
ここで、Z0は、Z3の接続端子から電源側をみたインピーダンスです。
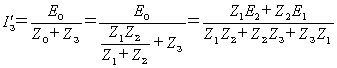 ------ (18)
------ (18)
但し、Z0=Z1Z2
/ (Z1+Z2)
![]() ------ (19)
------ (19)
![]() ------ (20)
------ (20)
(ニ)の電流( (ニ)=(ロ)+(ハ) として求める )
![]() ------ (21)
------ (21)
![]() ------ (22)
------ (22)
![]()
![]() ------ (23)
------ (23)
求める各回路の電流(I1,I2,I3)は、(21)、(22)、(23)式のとおり、キルヒホッフの法則により求めた電流(4),(5),(6)式と同じになる。
一般に、テブナンの理を用いる場合、I'3を求めることが多く、今回のようにI1,I2,I3まで計算するケースは実務面では少ないようです。
なお、(21),(22),(23)式は、途中の経過を少し省略して記載しています。
① それぞれの方法の特徴や活用方法は、概ね、以下のとおりです。
- キルヒホッフの法則による方法
最も基本的な計算方法であり、一般的に使用されている。
しかしながら、複雑な回路では計算が困難になる場合があります。 - 重ねの理による方法
電源(または、電流源)を1個づつに分けて計算するので、結果として、簡単になる場合があります。 - テブナンの理による方法
一般には、ある回路を接続(または事故発生)したときのその回路に流れる電流(第3図では、Z3を流れる電流)を求めるときに使う場合が多い。ここでは、変化前の電流と変化分の電流に分けて計算する方法を説明しています。ぜひ、双方の使い方を身に付けて欲しい。
② 重ねの理を説明する場合、R,L,C などの回路の定数が一定であること(線形であること)や電圧源・電流源について触れていますが、ここでは簡単のため使い方を中心に説明しています。
③ テブナンの理は、考え方は重ねの理を用いて説明できますが、ここでは違いが明確になるように、同じ回路で計算することに重点をおいています。このため、少し無理な説明部分がありますが、実用的な違いは把握いただけたと思います。


