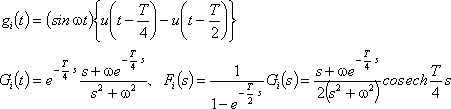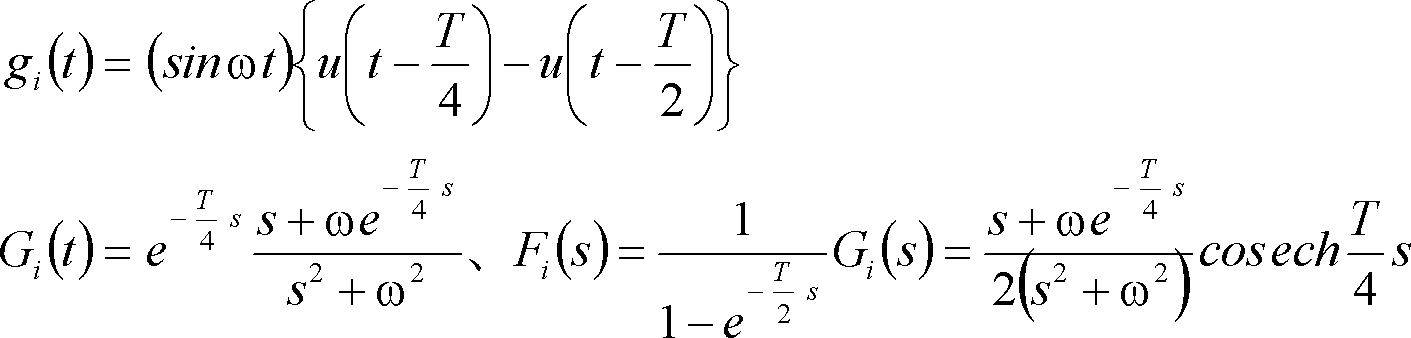〜終わり〜
■ぜひアンケートにご協力下さい■


電磁気現象は微分方程式で表され、一般的には微分方程式を解くための数学的に高度の知識が要求される。ラプラス変換は、計算手順さえ覚えれば、代数計算と変換公式の適用により微分方程式が解ける数学知識への負担が少ない解法である。このシリーズでは電気回路の過渡現象や制御工学等の分野での使用を念頭に置いて範囲を限定して、ラプラス変換を用いて解く方法を解説する。今回は、代表的非正弦波形の過渡現象の解き方について解説する。
① (1)式で定義された関数u(t)を単位ステップ関数といい、図示すると第1図(a)となる。
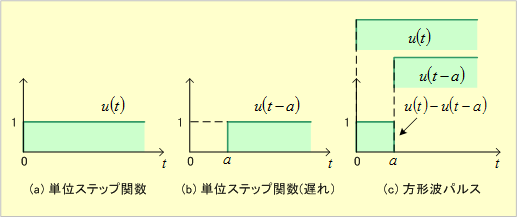
第1図 単位ステップ関数
② したがって、u(t−a)は、(2)式の性質があり、そのグラフは第1図(b)のようになる。
③ これらの性質を応用すると、
![]()
![]() は(3)式の関係があり、そのグラフは第1図(c)のようになる。
は(3)式の関係があり、そのグラフは第1図(c)のようになる。
④
![]()
![]() であるとき、
であるとき、
![]()
![]() は(4)式の関係にある。図示すると第2図(a)であり、ab区間のみが単位量なので、これを単位区間関数と呼ぶことにする。
は(4)式の関係にある。図示すると第2図(a)であり、ab区間のみが単位量なので、これを単位区間関数と呼ぶことにする。
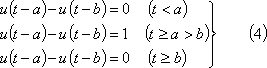
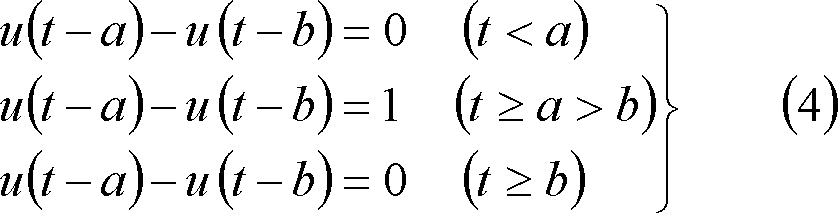
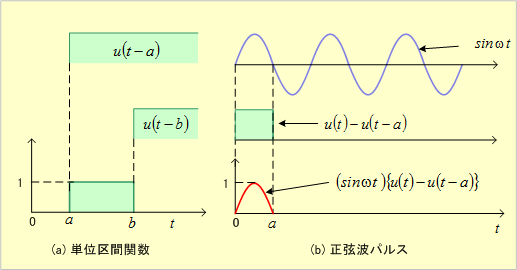
第2図 単位ステップ関数の応用
⑤ 正弦波形sinωtの最初の正波(第2図(b)の赤い波形)は、(5)式のように、正弦波形と単位区間関数との積で表示できる。
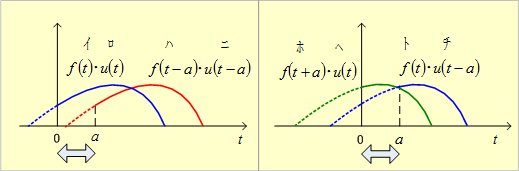
第3図 t推移法則(1) 第4図 t推移法則(2)
t推移法則とは 『第3図のように時間関数
![]()
![]() を時間的に
を時間的に
![]()
![]() だけ遅らせた関数
だけ遅らせた関数
![]()
![]() のラプラス変換は、
のラプラス変換は、
![]()
![]() のラプラス変換である
のラプラス変換である
![]()
![]() の
の
![]()
![]() 倍に等しい』というものである。
倍に等しい』というものである。
いま、
![]()
![]() とおけば、この関係は、(6−1)、(6−2)式に示す結果となり、t推移法則は(6)式で表示でき、(7)式のようにも書ける。
とおけば、この関係は、(6−1)、(6−2)式に示す結果となり、t推移法則は(6)式で表示でき、(7)式のようにも書ける。
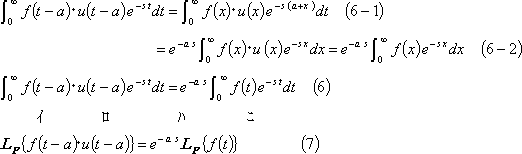
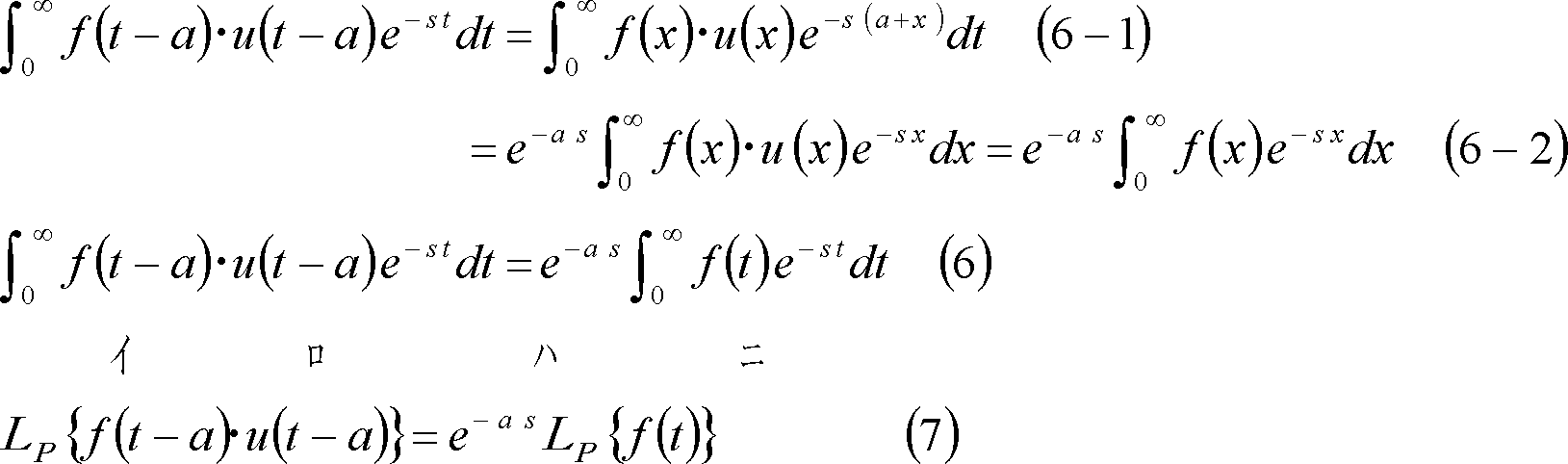
また、t推移法則は(8)式で示す関係にあり(9)式が成立する。(第4図参照)。
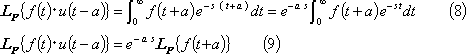
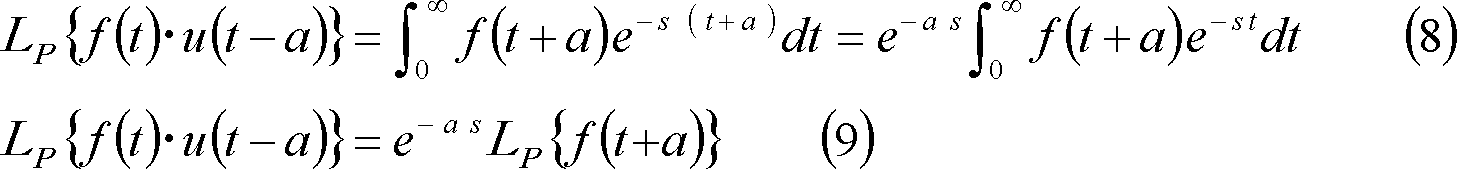
[注]もう一つの推移法則であるs推移法則は、(10)式の関係から(11)式のように表示される。
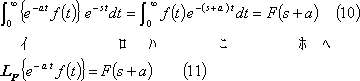
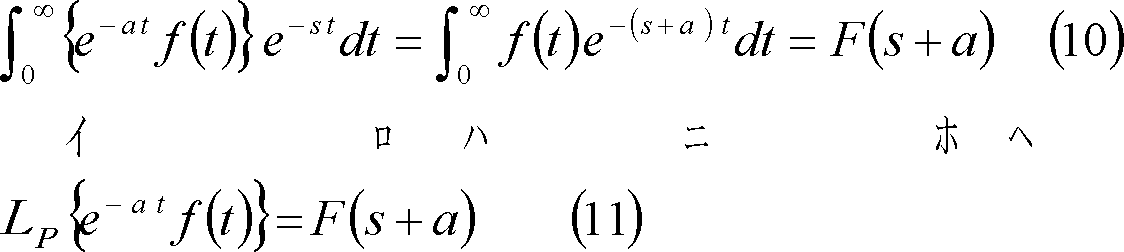
① ステップ関数で、a以降の区間のみ選択した関数
![]()
![]() のラプラス変換は、
のラプラス変換は、
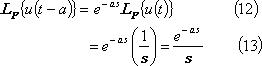
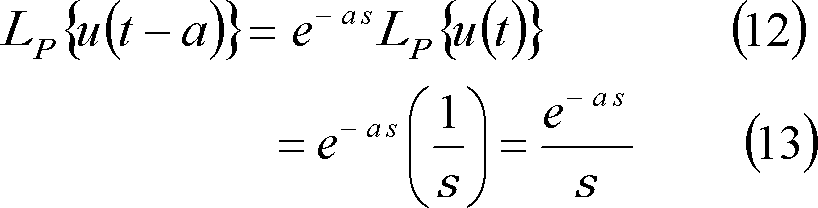
② f(t)のab区間のみ選択した関数
![]()
![]() のラプラス変換は、
のラプラス変換は、
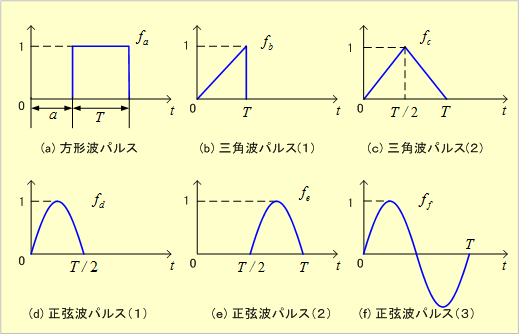
第5図 いろいろな波形
③ 方形波パルス・・・ 第5図(a)
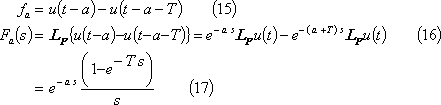
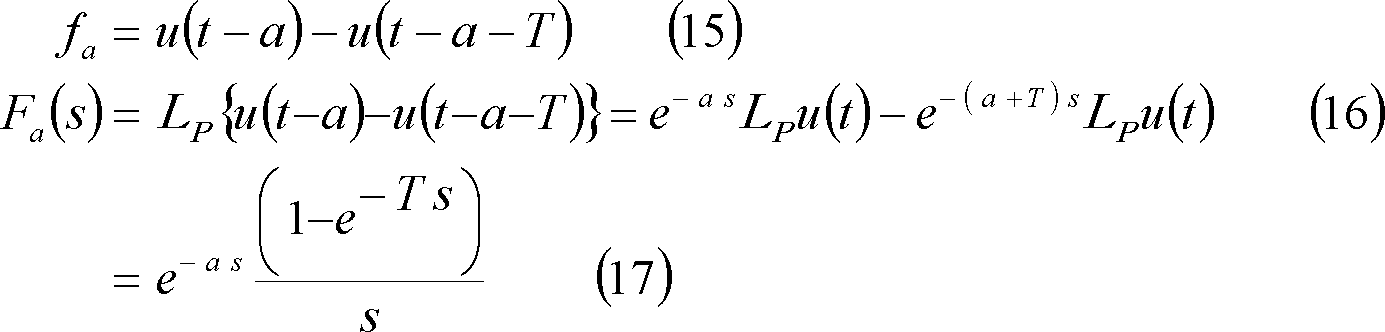
④ 三角波パルス(1)・・・ 第5図(b)
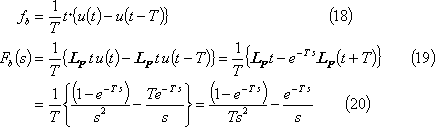
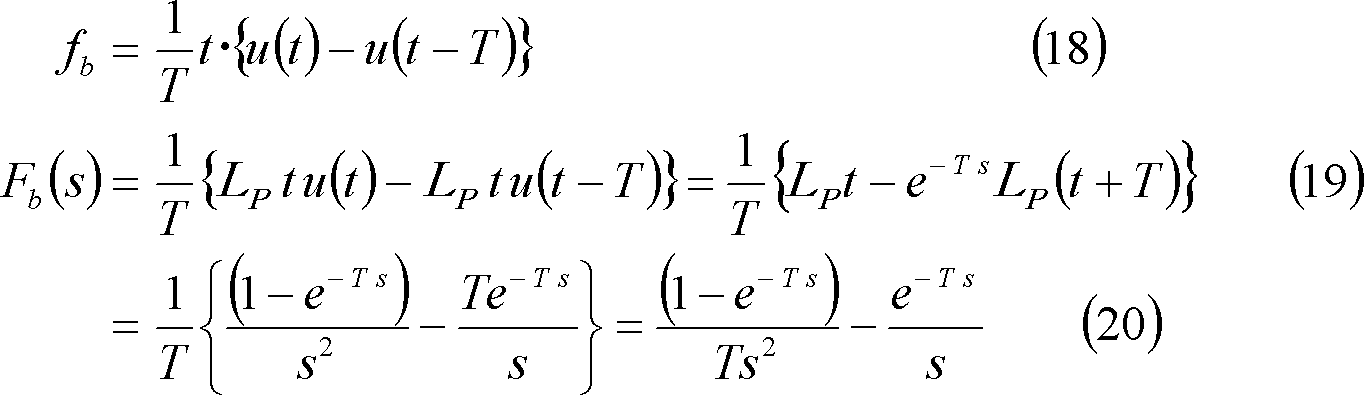
⑤ 三角波パルス(2)・・・ 第5図(c)
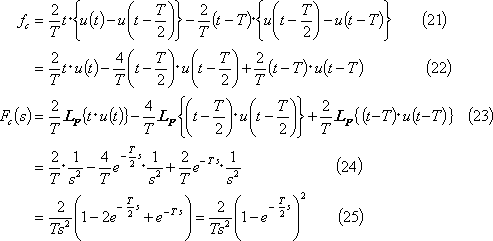
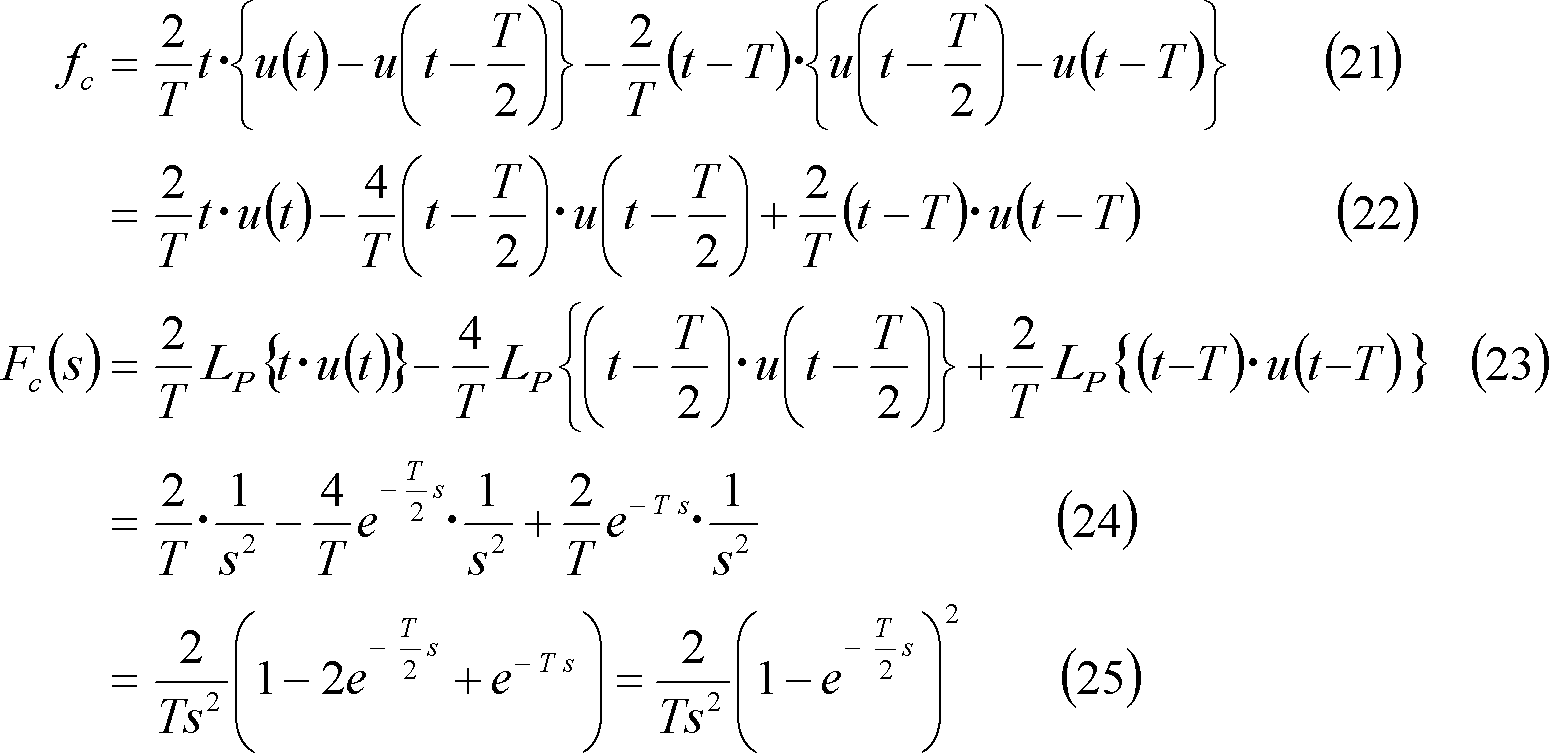
⑥ 正弦波パルス(1)・・・ 第5図(d)
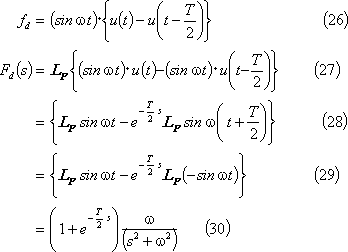
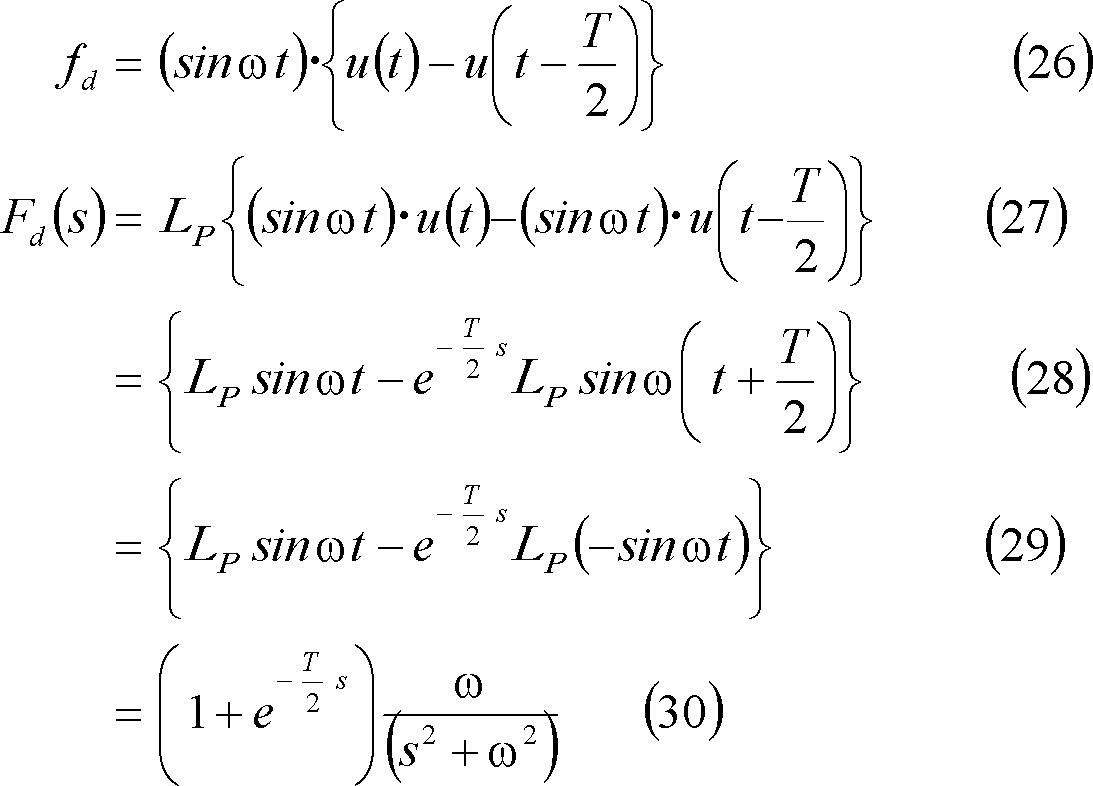
⑦ 正弦波パルス(2)・・・ 第5図(e)
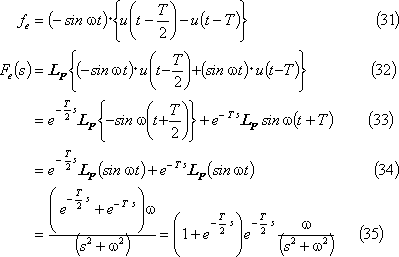
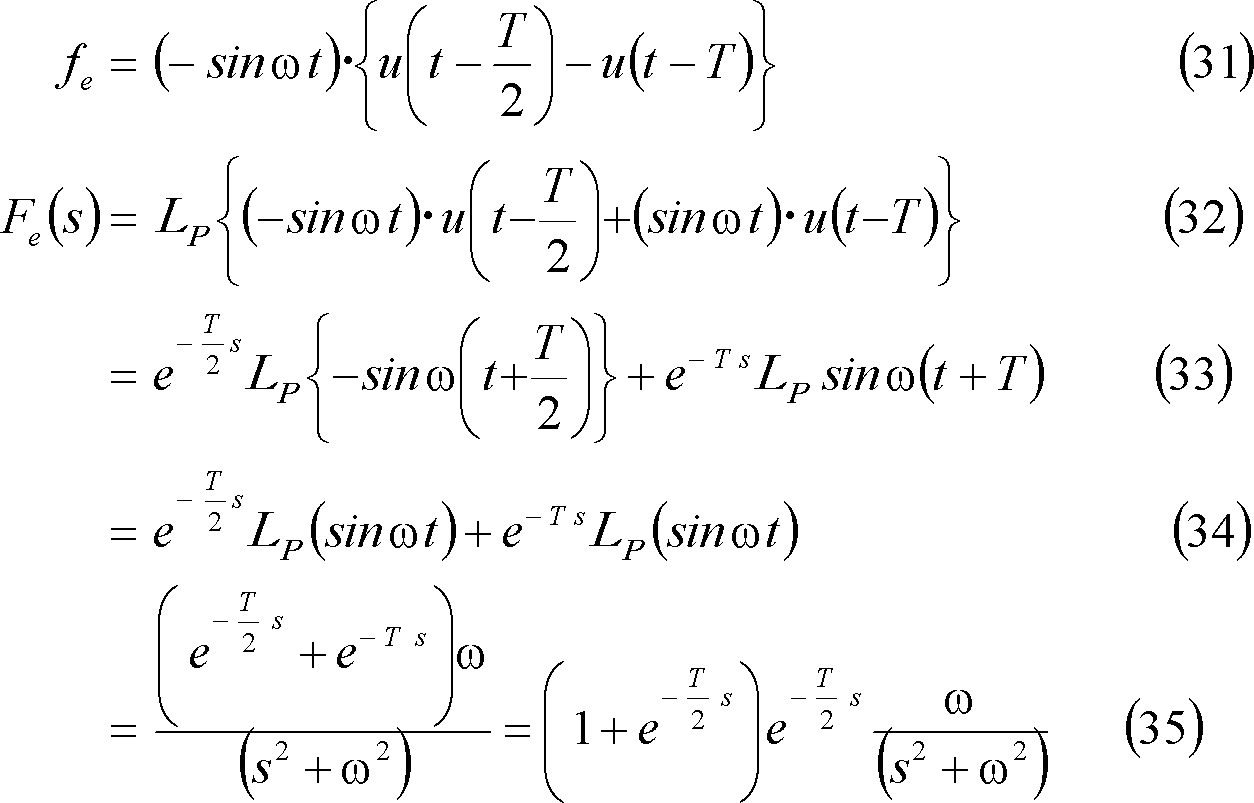
[別解] この波形は第5図(d)の波形より右に
![]()
![]() シフトした波形なので、t推移法則により、
シフトした波形なので、t推移法則により、
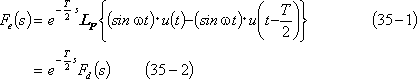
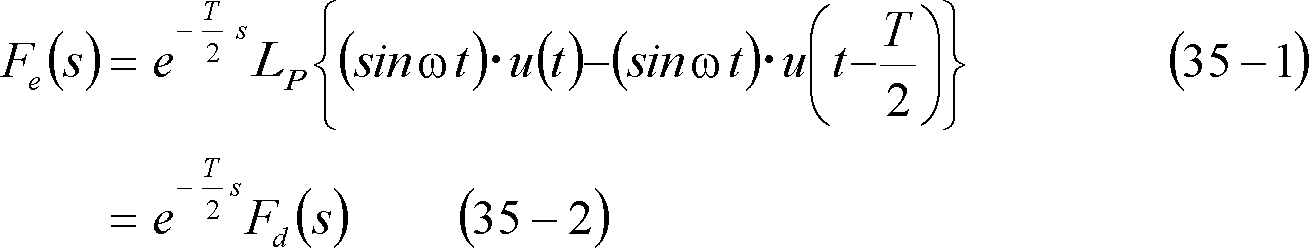
で、(35)式が求められる。
⑧ 正弦波パルス(3)・・・ 第5図(f)
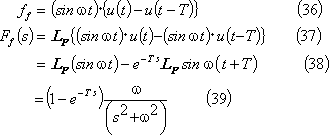
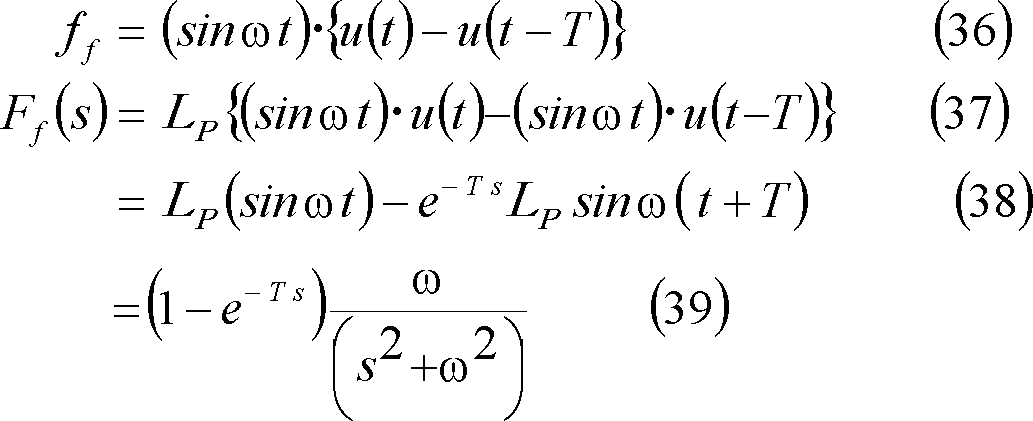
第6図のように、波形
![]()
![]() が周期Tで現れ、これが際限なく続く図のような波形(周期波)を
が周期Tで現れ、これが際限なく続く図のような波形(周期波)を
![]()
![]() とすれば、
とすれば、
![]()
![]() のラプラス変換は次式となる。
のラプラス変換は次式となる。
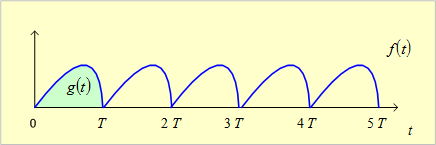
第6図 周期波
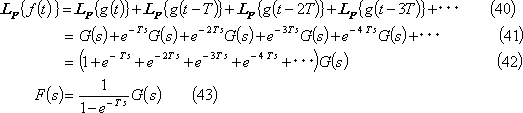
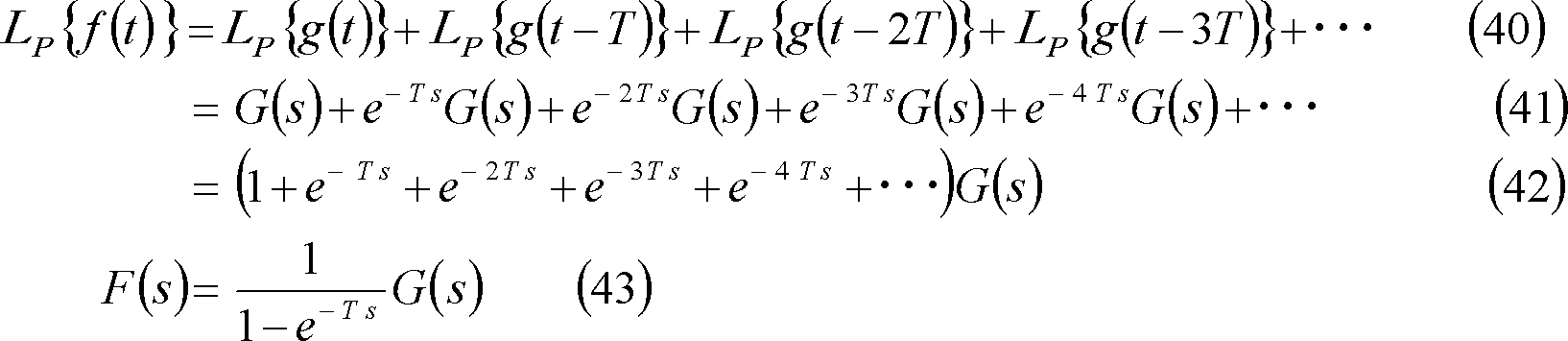
したがって、第7図に示す波形のラプラス変換は次のように求められる。
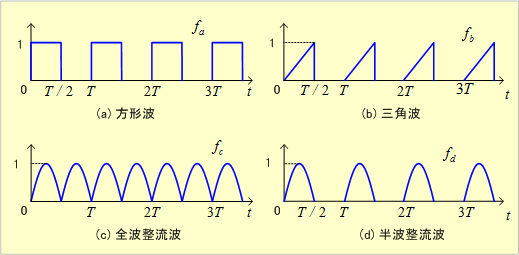
第7図 各種の周期波
① 方形波・・・第7図(a)
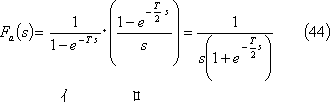
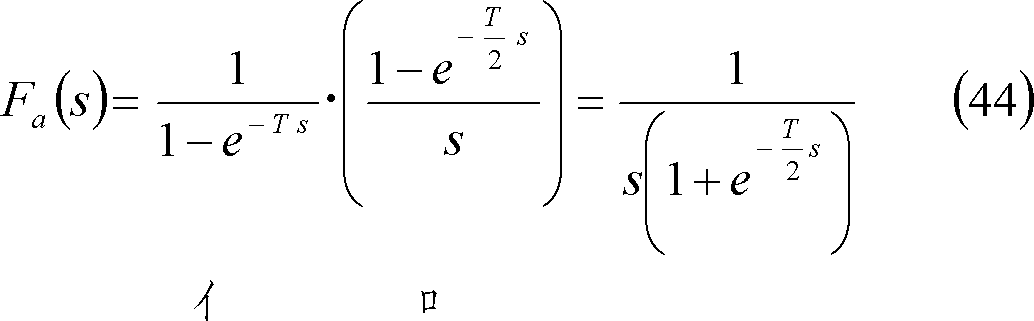
② 三角波・・・第7図(b)
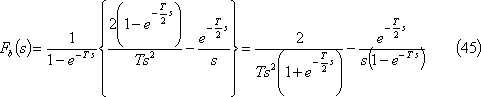
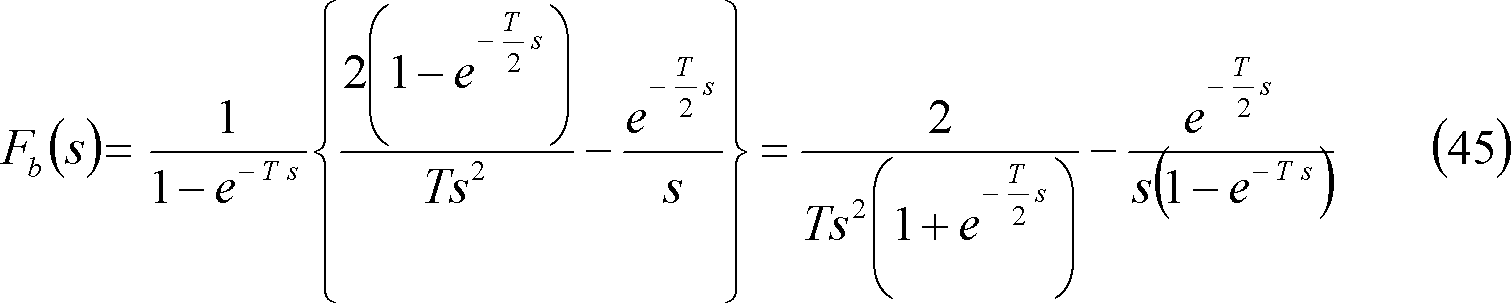
③ 全波整流波・・・第7図(c)
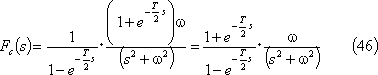
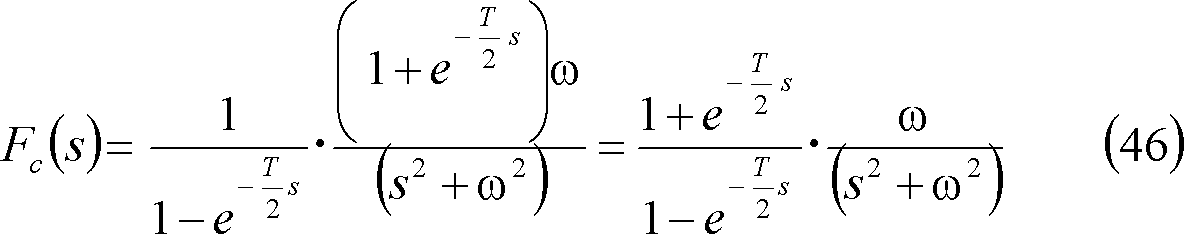
④ 半波整流波・・・第7図(d)
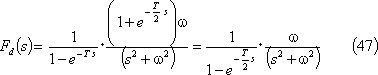
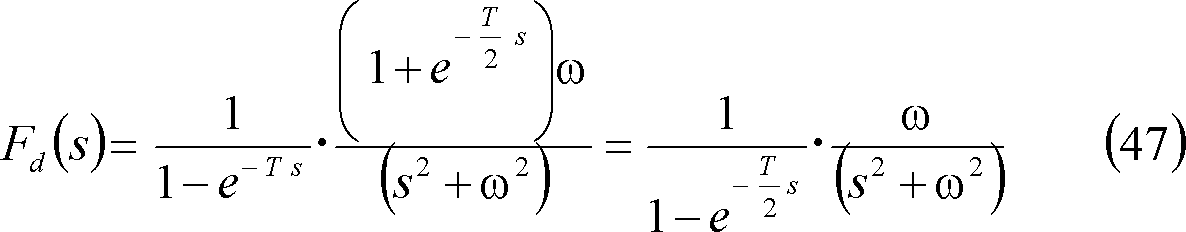
問題 第8図に示す各波形をラプラス変換せよ。ただし、(d)図以降は周期波とする。
答の巻末
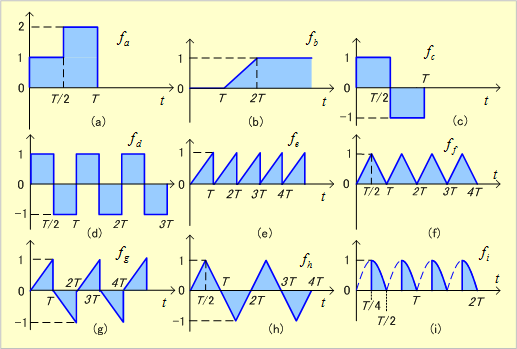
第8図
① RL直列回路
第9図(a)のRL直列回路において、同図(b)に示すような起電力e(t)を印加した時、回路に流れる電流を求めよ。
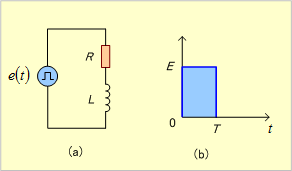
第9図 RL直列回路
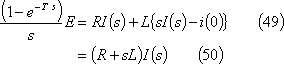
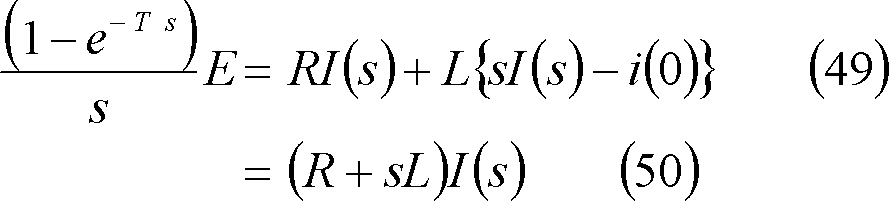
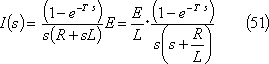
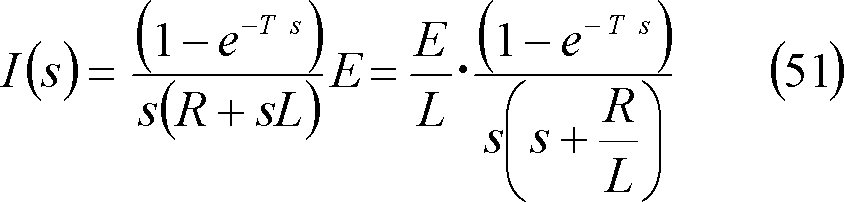
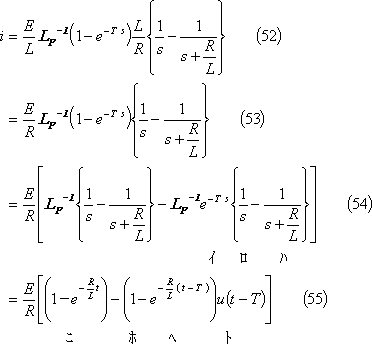
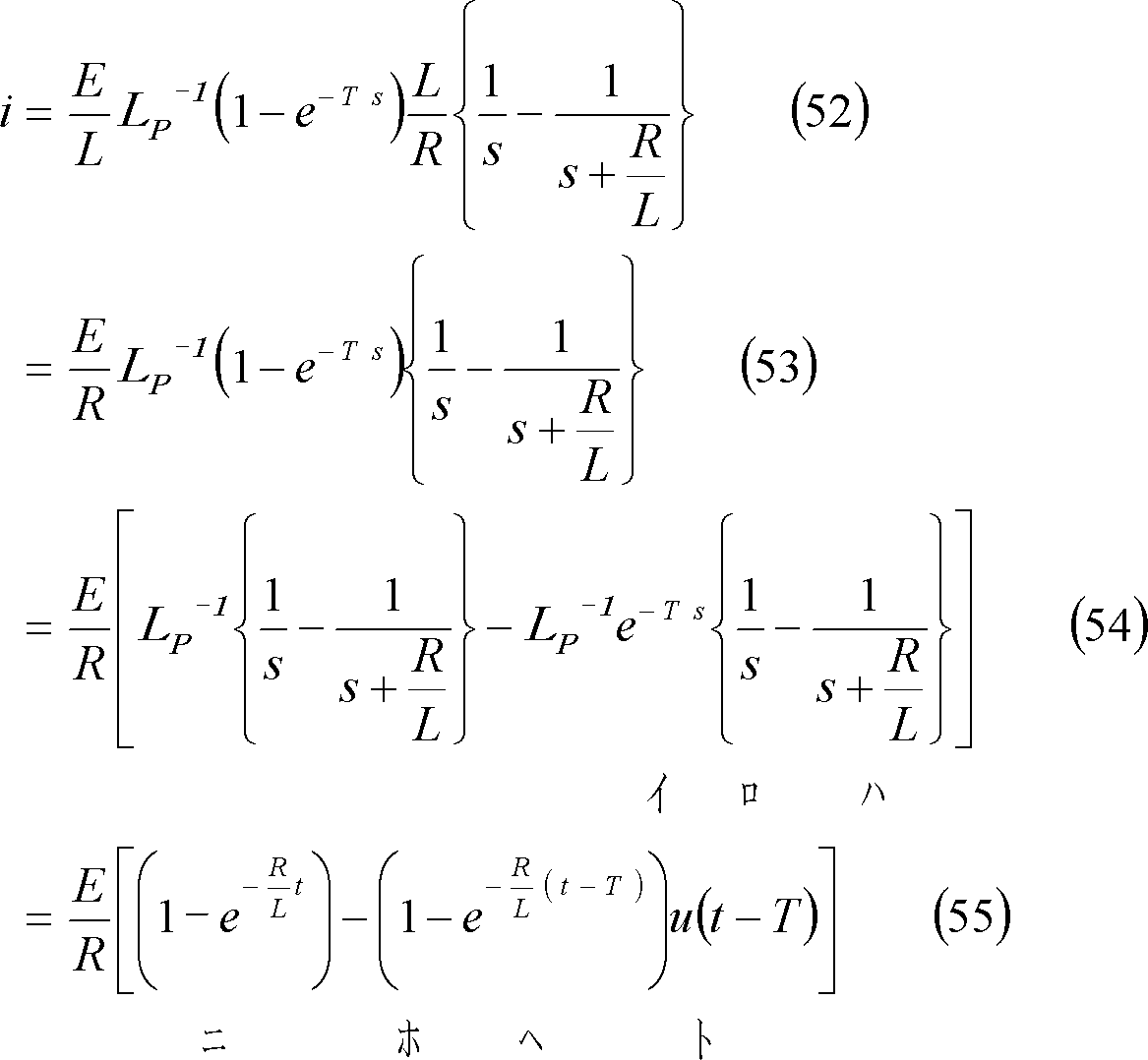
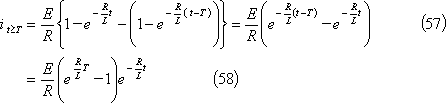
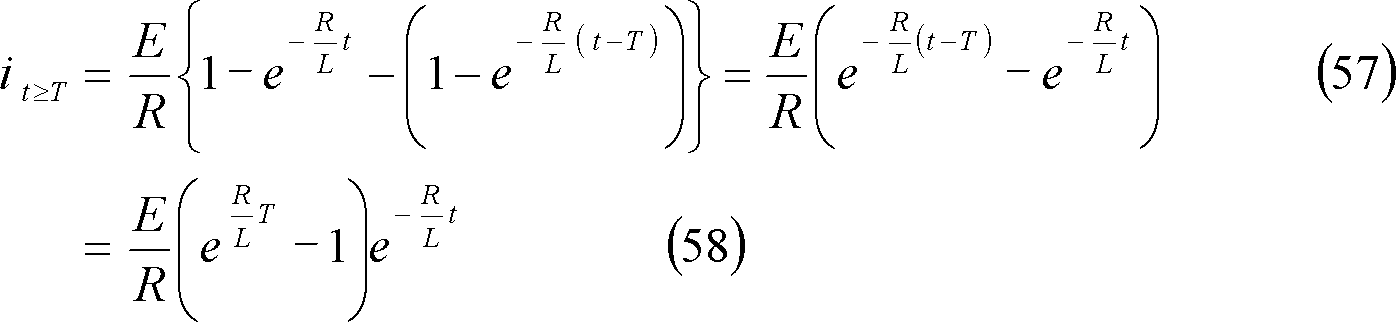
求める電流iのグラフは第10図となる。
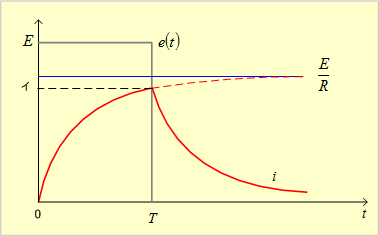
第10図 RL直列回路の電流
② RC直列回路
第11図(a)のRC直列回路において、同図(b)に示すような起電力e(t)を印加した時、回路に流れる電流を求めよ。
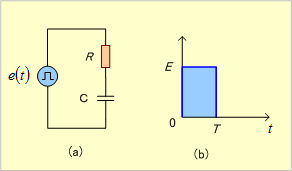
第11図 RC直列回路
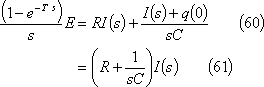
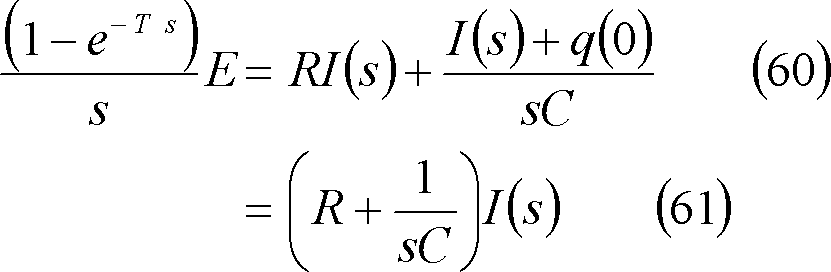
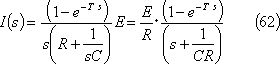
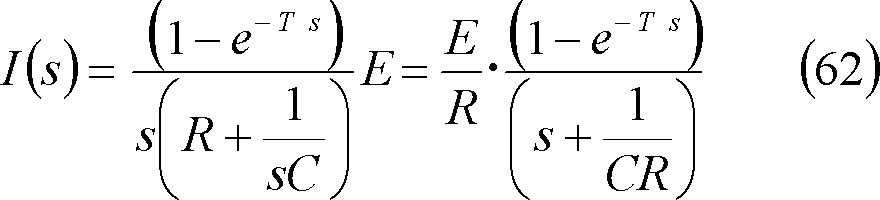
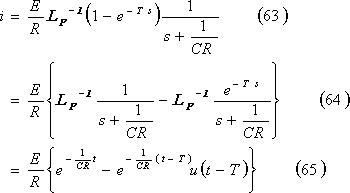
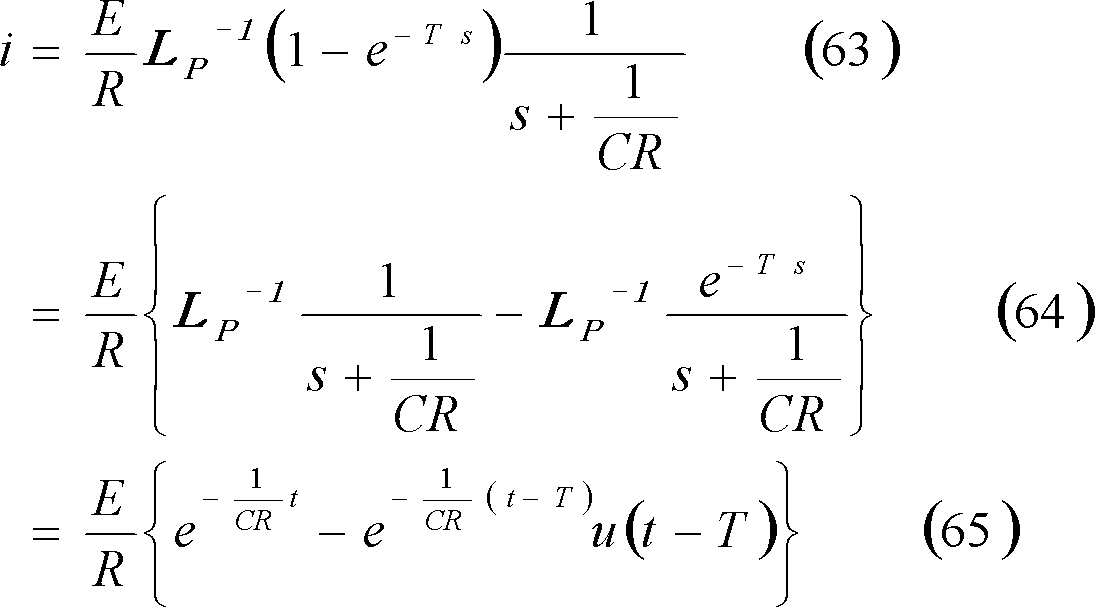
求める電流iのグラフは第12図となる。
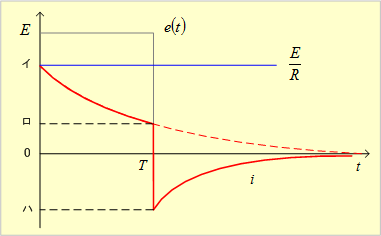
第12図 RC直列回路の電流
① 微分回路
第13図(a)の回路で、
![]()
![]() として同図(b)のような方形波(周期波)を印加した時、R端の電圧
として同図(b)のような方形波(周期波)を印加した時、R端の電圧
![]()
![]() に注目すると、両者の関係は、
に注目すると、両者の関係は、
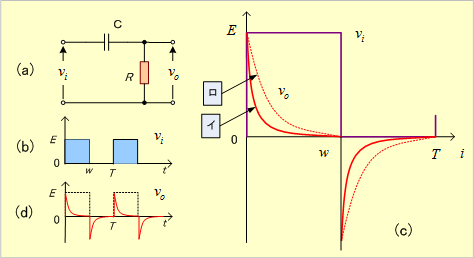
第13図 微分回路
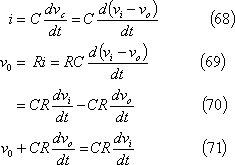
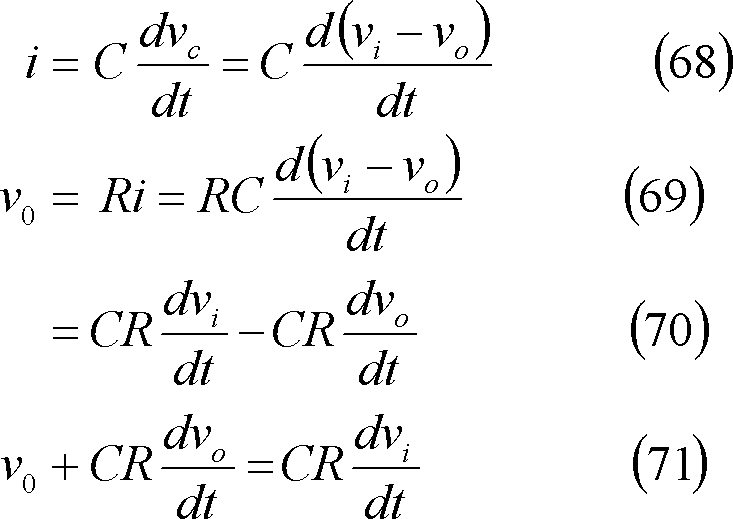
もし、上式で
![]()
![]() の関係にあれば、
の関係にあれば、
となる。第13図(c)は
![]()
![]() 一周期の波形で、時定数を小さくするにつれてロからイの方に移り、(73)式を実現する『出力電圧は入力電圧の微分値に比例した電圧』が得られる。このような機能をもった回路を微分回路という。第13図(d)には同図(b)の周期波
一周期の波形で、時定数を小さくするにつれてロからイの方に移り、(73)式を実現する『出力電圧は入力電圧の微分値に比例した電圧』が得られる。このような機能をもった回路を微分回路という。第13図(d)には同図(b)の周期波
![]()
![]() 対する
対する
![]()
![]() の波形を示す。
の波形を示す。
② 積分回路
第14図(a)の回路において、
![]()
![]() として図(b)のような方形波(周期波)を印加した時、C端の電圧
として図(b)のような方形波(周期波)を印加した時、C端の電圧
![]()
![]() に注目すると、両者の関係は、
に注目すると、両者の関係は、
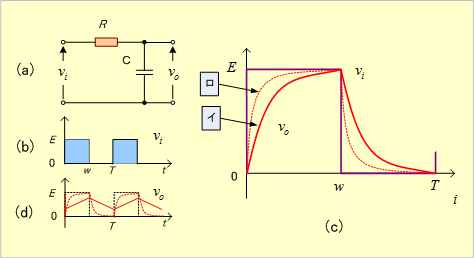
第14図 積分回路
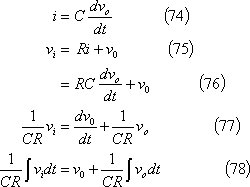
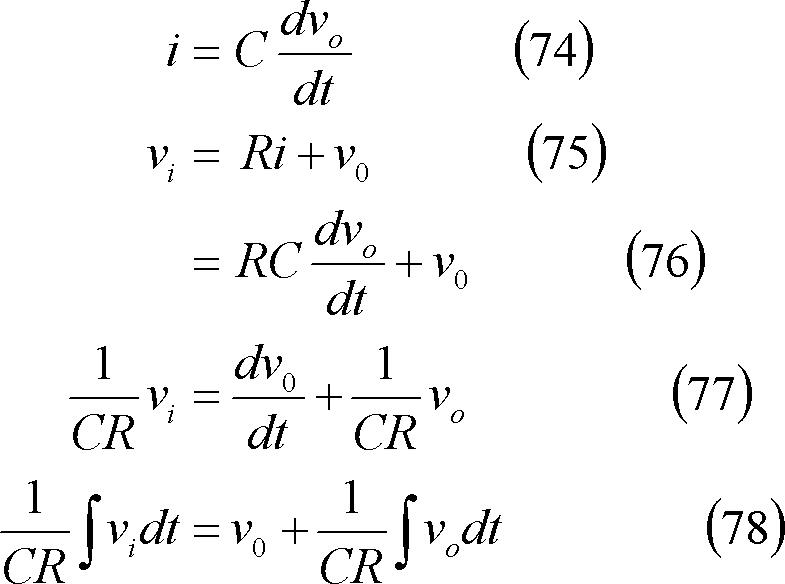
もし、上式で
![]()
![]() の関係にあれば、
の関係にあれば、
となる。第14図(c)は
![]()
![]() 一周期の波形で、時定数を大きくするにつれてロからイの方に移り、(80)式を実現する『出力電圧は入力電圧の積分値に比例した電圧』が得られる状態になる。このような機能をもった回路を積分回路という。第14図(d)には時定数を充分大きくした場合の、同図(b)の周期波
一周期の波形で、時定数を大きくするにつれてロからイの方に移り、(80)式を実現する『出力電圧は入力電圧の積分値に比例した電圧』が得られる状態になる。このような機能をもった回路を積分回路という。第14図(d)には時定数を充分大きくした場合の、同図(b)の周期波
![]()
![]() に対する
に対する
![]()
![]() の波形を示す。
の波形を示す。
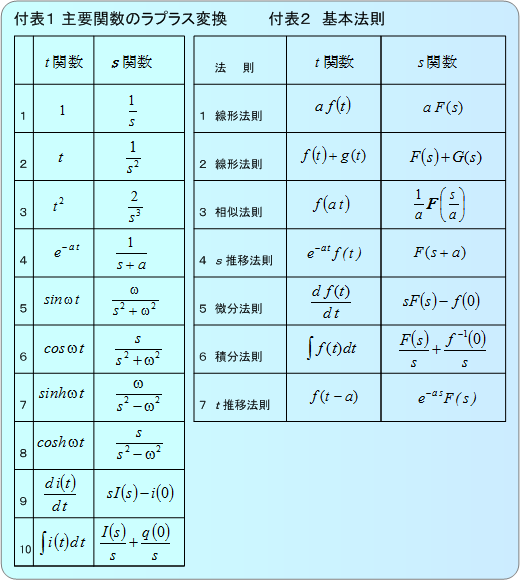
【付表】
【問題の答】
(a)
![]()
![]()
(b)
![]()
![]()
(c)
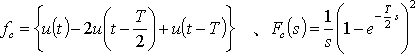
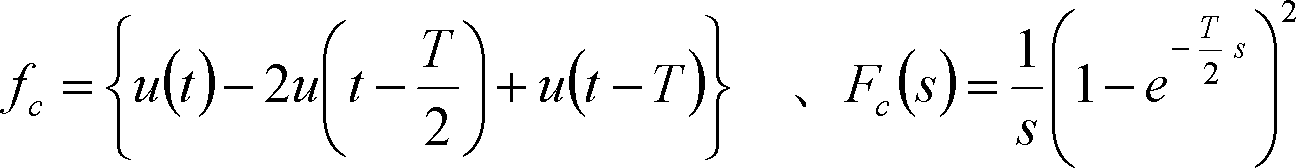
(d)
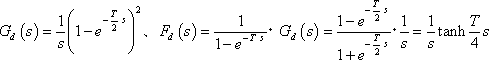
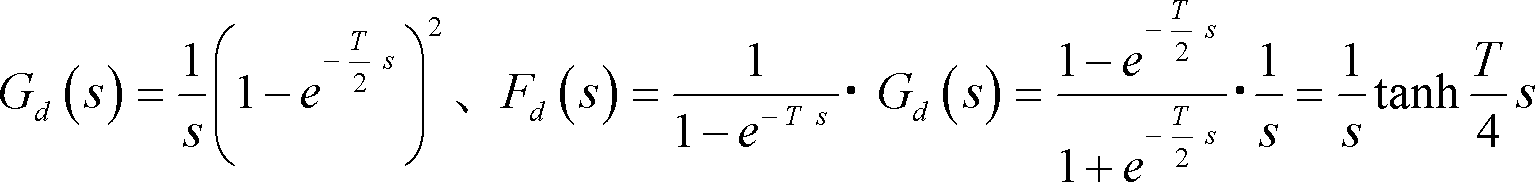
(e)
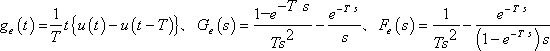
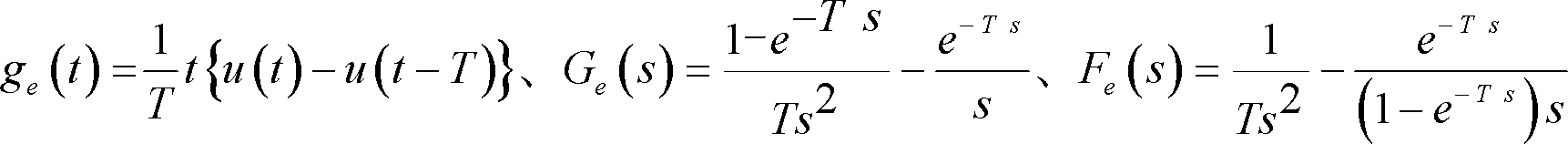
(f)
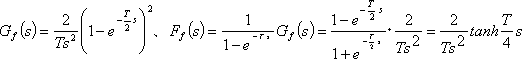
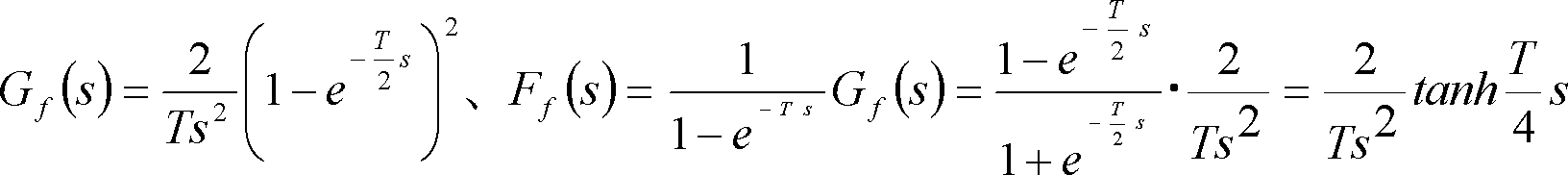
(g)
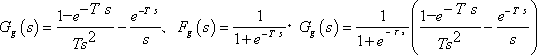
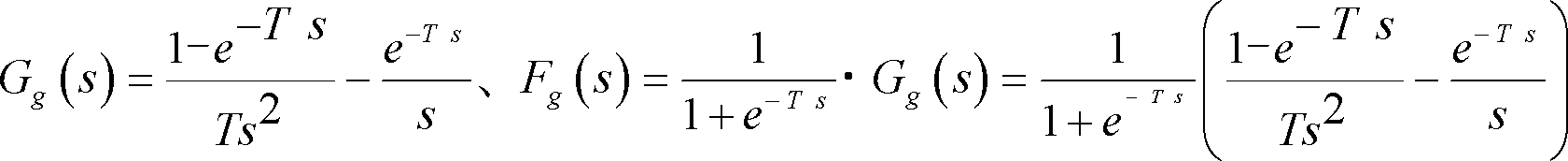
(h)
![]()
![]()
(i)