〜終わり〜
■ぜひアンケートにご協力下さい■


電磁気現象は微分方程式で表され、一般的には微分方程式を解くための数学的に高度の知識が要求される。ラプラス変換は、計算手順さえ覚えれば、代数計算と変換公式の適用により微分方程式が解ける数学知識への負担が少ない解法である。このシリーズでは電気回路の過渡現象や制御工学等の分野での使用を念頭に置いて範囲を限定して、ラプラス変換を用いて解く方法を解説する。今回は、ラプラス変換とはどんな計算法なのかを概観し、この計算法における基礎事項について解説する。
私たちが扱う電気回路は、電圧や電流などの電気的諸量を時間の関数として表す。そしてこれらの時間関数(t関数)からなる回路方程式(微分方程式)を解くのであるが、この方程式にラプラス変換という数学的操作を加えて別の関数(s関数)に変換し、s関数相互間の関係として計算し、その計算結果(s関数)を、ラプラス逆変換という数学的操作によりt関数に戻して答を知ろうというのである。その計算のイメージは第1図のようになる。
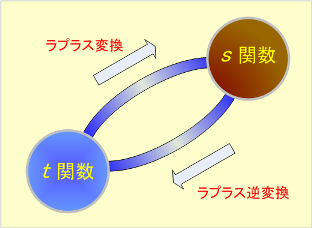

第1図 ラプラス変換の計算イメージ
例えば、抵抗RとインダクタンスLとの直列回路に直流電圧Eを印加した場合、回路に流れる電流iを求めるというケースついて示すと、その計算の流れは第2図となる。
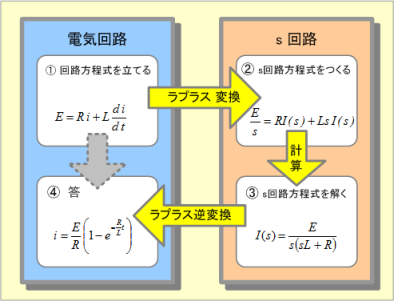

第2図 ラプラス変換の計算フロー
したがって、ラプラス変換による「電気回路の解き方」の計算手順は次の4ステップである。
手順1 対象となる回路について、t関数による電圧方程式を立てる。(電圧方程式)
手順2 電圧方程式の諸量をラプラス変換し、s回路方程式をつくる。(ラプラス変換)
手順3 s回路方程式を求めている量のs関数X(s)について解く。(s回路計算)
手順4 X(s)をラプラス逆変換して、答であるx(t)を得る。(ラプラス逆変換)
いま、時間関数
![]()
![]() があるとき、
があるとき、
のように計算したものを
![]()
![]() のラプラス変換という。
のラプラス変換という。
つまり、
![]()
![]() を「t=0から∞まで時間積分する」という数学的な加工を施したものを「f(t)のラプラス変換」と呼ぶことにするのである。
を「t=0から∞まで時間積分する」という数学的な加工を施したものを「f(t)のラプラス変換」と呼ぶことにするのである。
ラプラス変換の計算イメージとしては、例えばf(t)が一定値Aであった場合は、そのラプラス変換は第3図のようになり、図中の緑色部がラプラス変換した値となる。
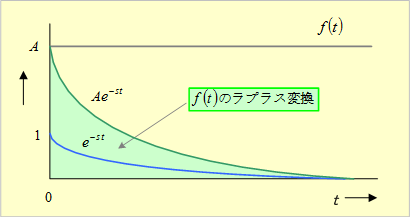

第3図 ラプラス変換の計算イメージ
計算式によれば、
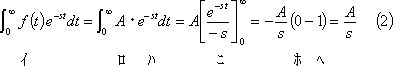
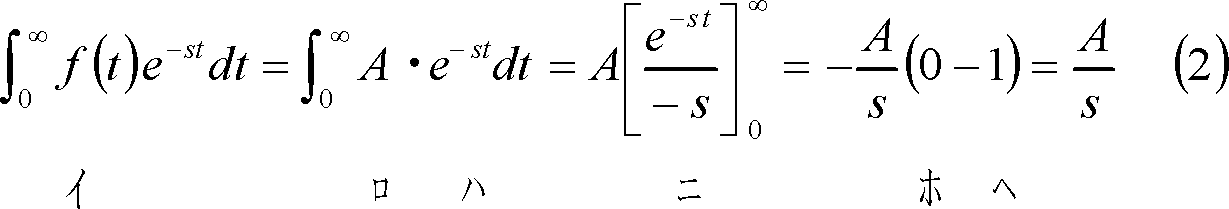
となる。したがって、この計算例から分かるように、ラプラス変換の計算結果は、一般的にsの関数となるので、これからは
![]()
![]() のラプラス変換を
のラプラス変換を
![]()
![]() と表すことにする。つまり、
と表すことにする。つまり、
である。
(1) 時間関数が定数の場合
定数の単位量をとりあげ
![]()
![]() の場合を考える。この場合は第3図においてA=1の場合なので、そのラプラス変換は次式のようになる。
の場合を考える。この場合は第3図においてA=1の場合なので、そのラプラス変換は次式のようになる。
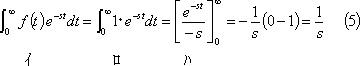
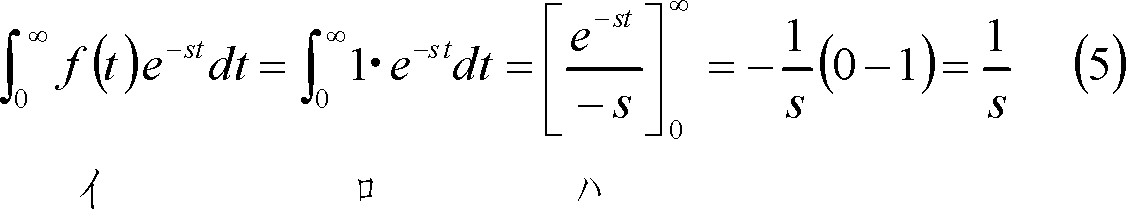
(2) 時間関数がべき関数の場合
①
![]()
![]() の場合は、部分積分法を使用して次のようになる。
の場合は、部分積分法を使用して次のようになる。
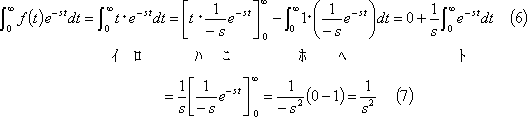
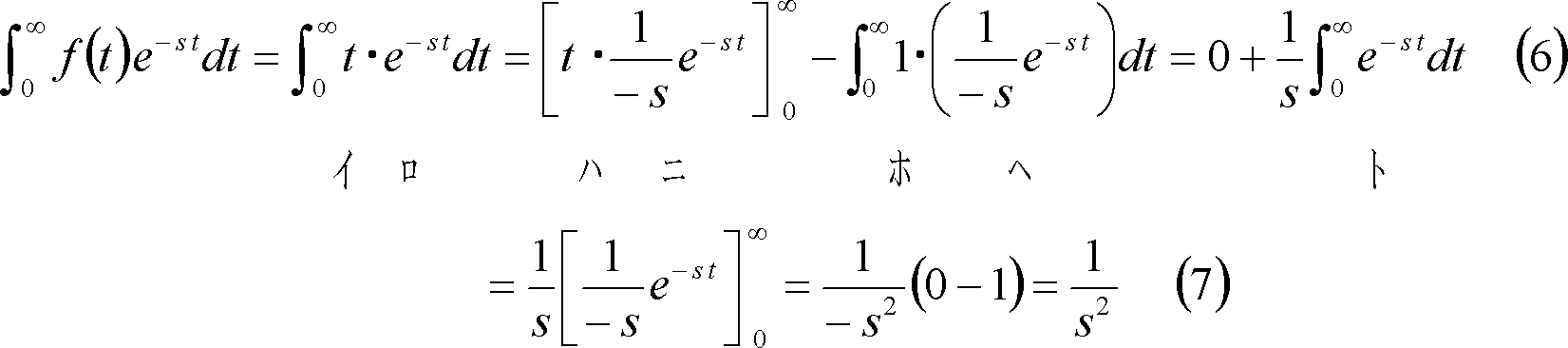
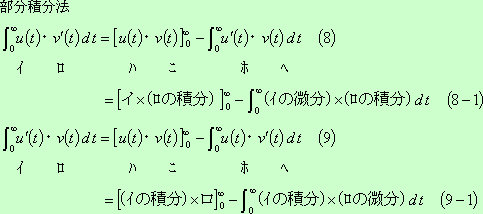
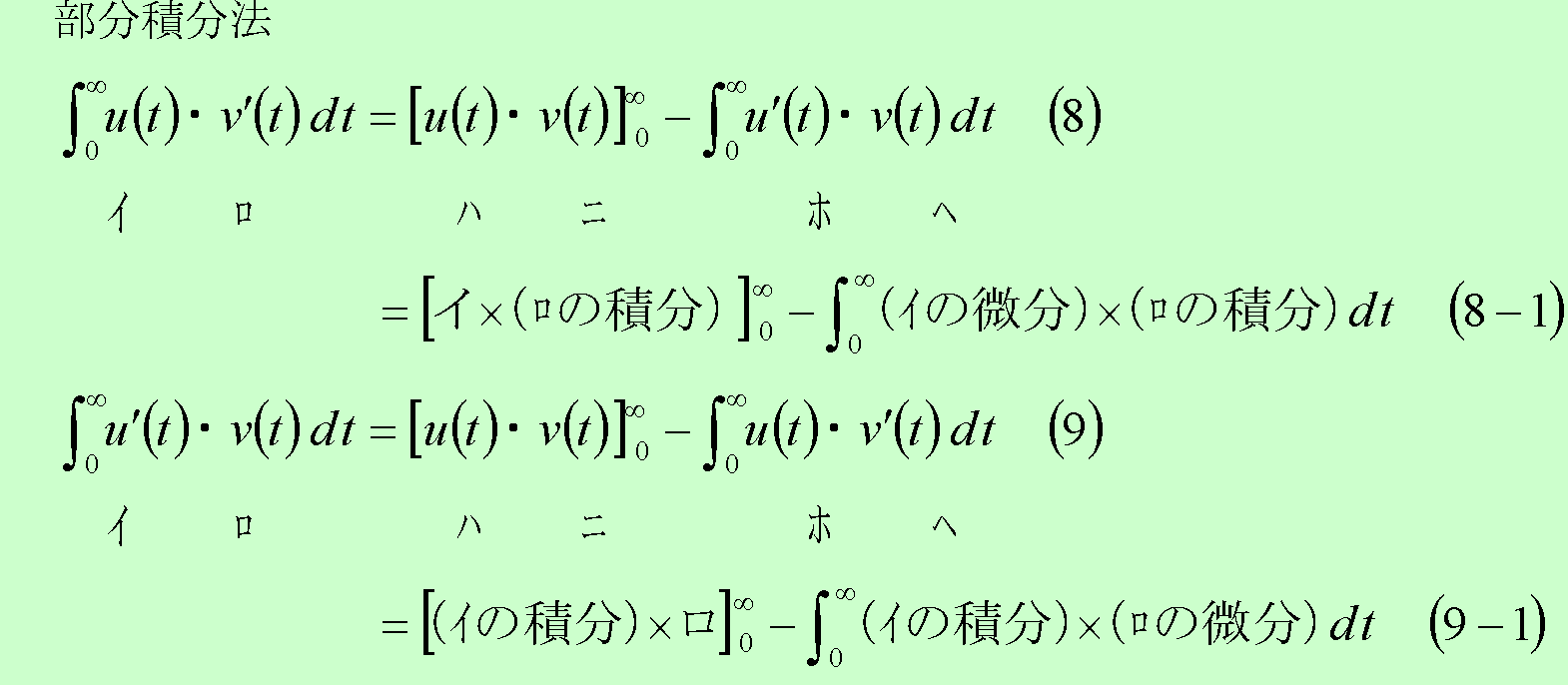
②
![]()
![]() の場合は、
の場合は、
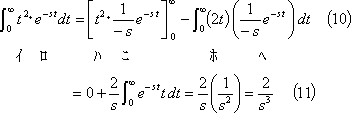
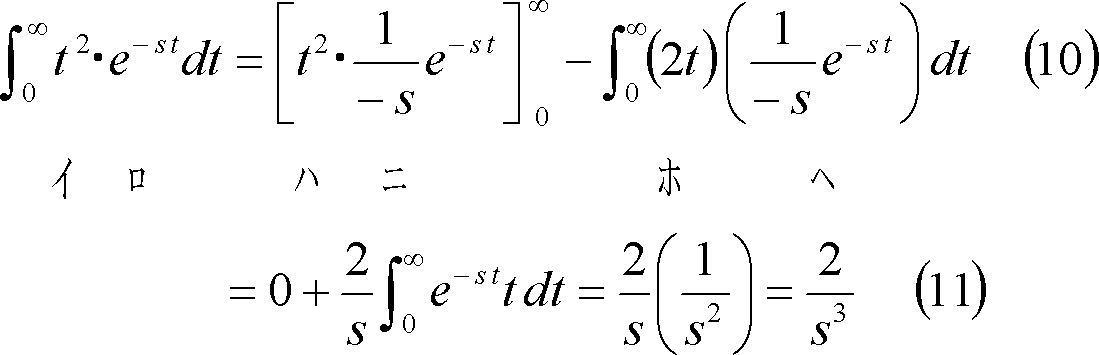
(3) 時間関数が指数関数の場合
![]()
![]() の場合は、
の場合は、
(4) 時間関数が三角関数の場合
①
![]()
![]() の場合は、
の場合は、
の関係にあるので、
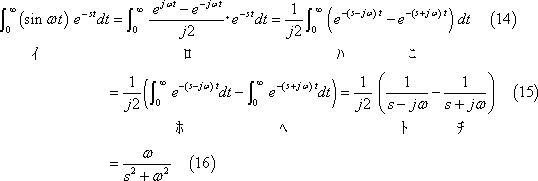
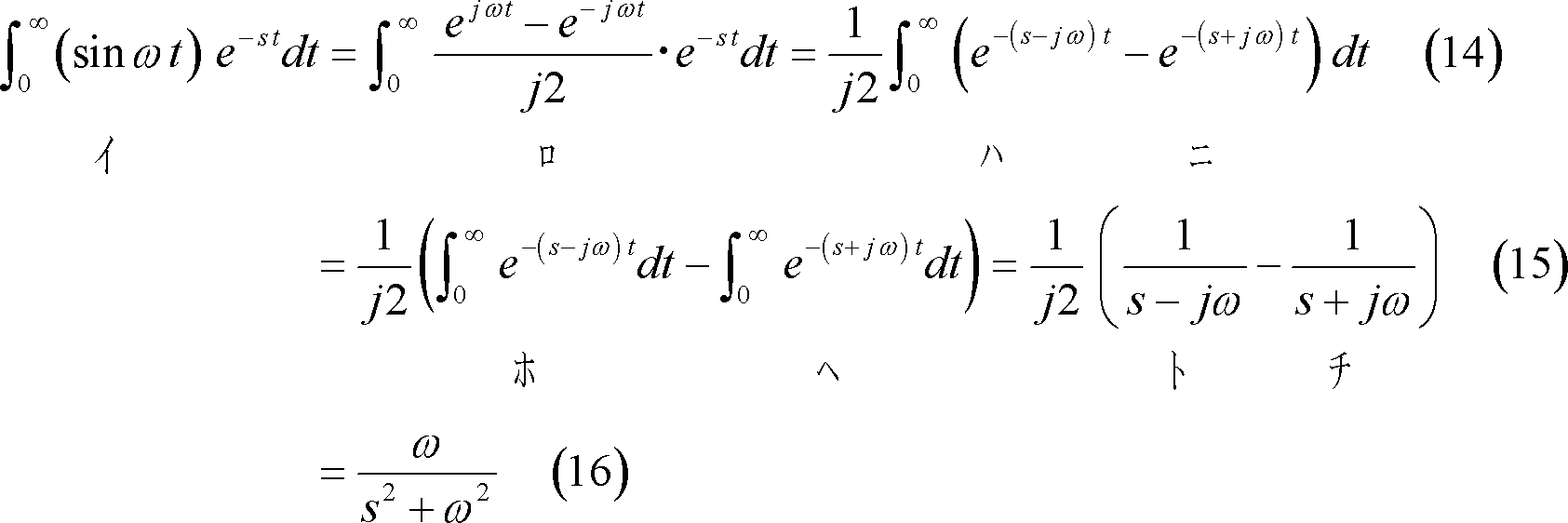
②
![]()
![]() の場合は、
の場合は、
の関係にあるので、
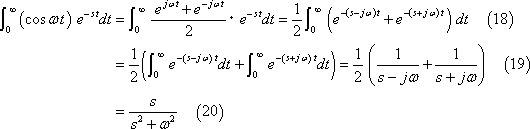
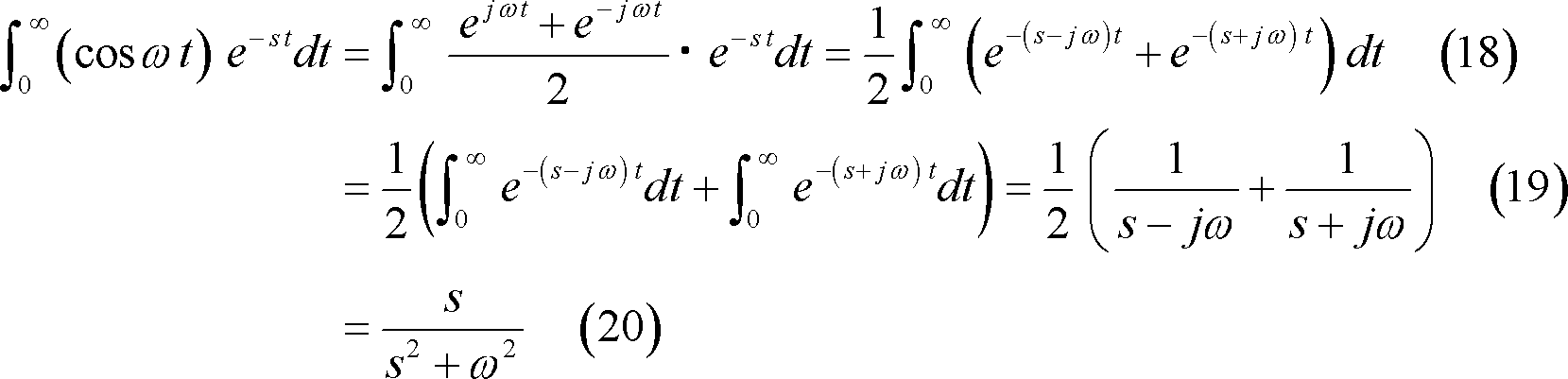
(5) 時間関数が双曲線関数の場合
①
![]()
![]() の場合は、
の場合は、
の関係にあるので、
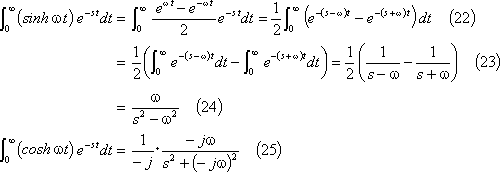
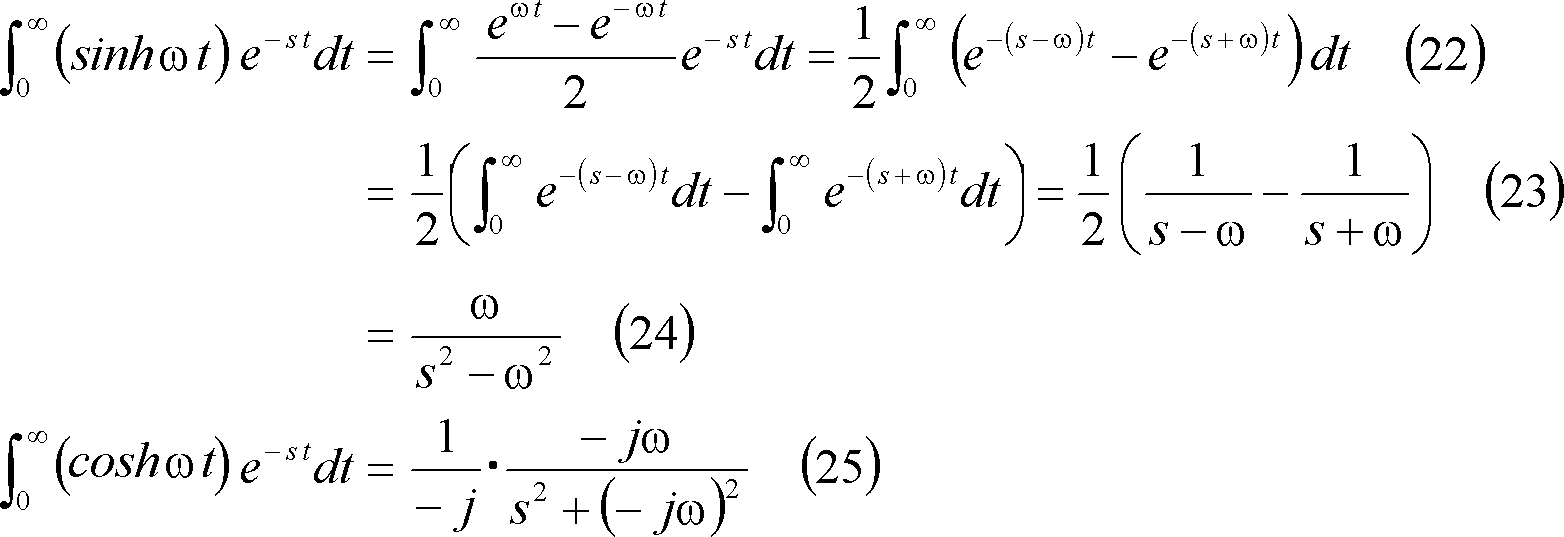
②
![]()
![]() の場合は、
の場合は、
の関係にあるので、
以上の計算で分かるように、時間関数をラプラス変換すると、その結果はsの関数となる。このため最も一般的な表記として、前にも述べたように時間関数f(t)のラプラス変換値をF(s)とする表記するのである。
つまり、
である。
(6) 時間関数が微分形関数の場合
①
![]()
![]() の時間微分
の時間微分
![]()
![]() を
を
![]()
![]() と表記すれば、
と表記すれば、
![]()
![]() のラプラス変換は部分積分法により、
のラプラス変換は部分積分法により、
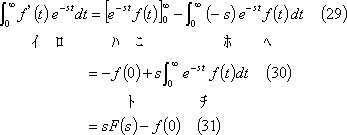
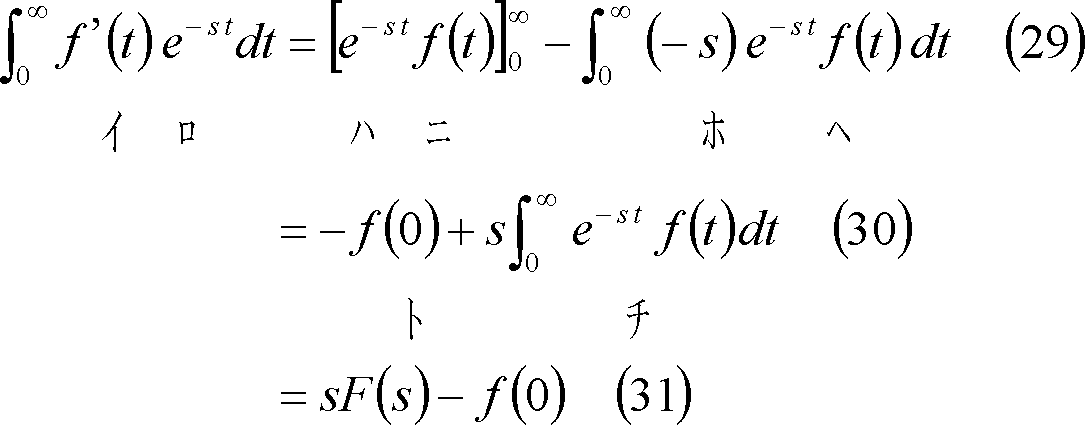
上式で
![]()
![]() は
は
![]()
![]() のt =0における値を表し、
のt =0における値を表し、
![]()
![]() の初期値という。
の初期値という。
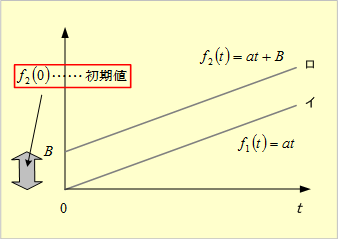

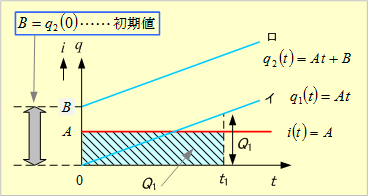
第4図 微分形関数
[例] 時間関数が電流
![]()
![]() である場合は、(31)式から、次式となる。
である場合は、(31)式から、次式となる。
② 時間関数が2階微分形である場合は、
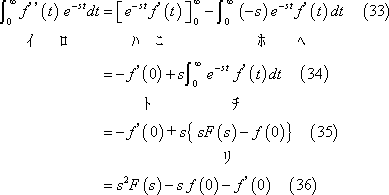
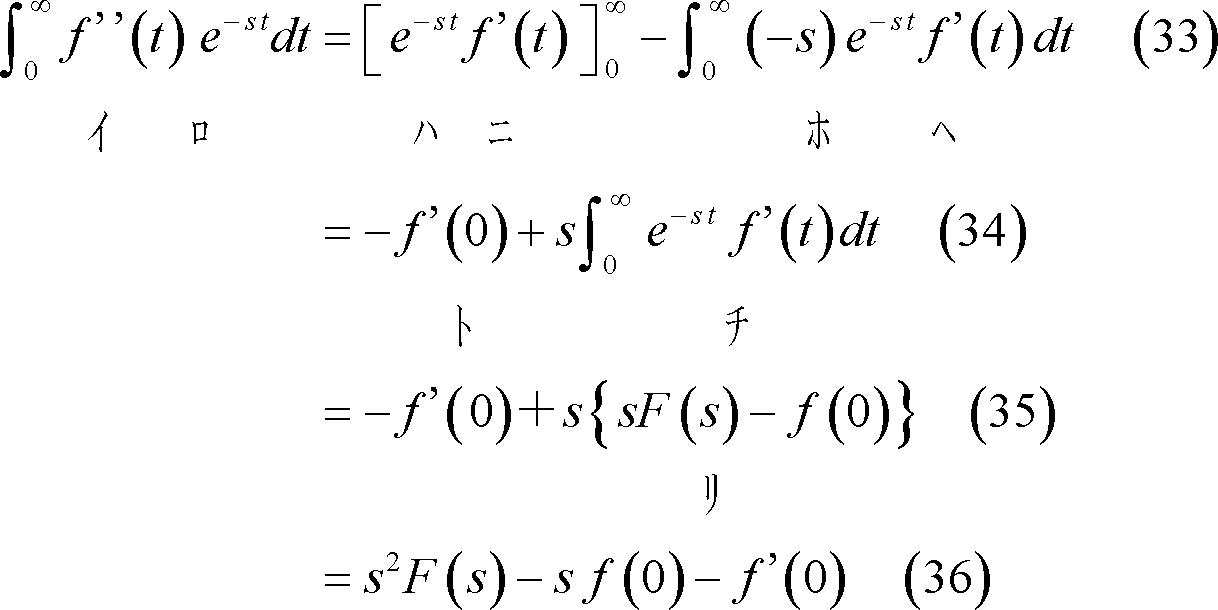
(7) 時間関数が積分形関数の場合
① ラプラス変換の対象が
![]()
![]() の時間積分である
の時間積分である
![]()
![]() の場合は、これを
の場合は、これを
![]()
![]() と表記すれば、
と表記すれば、
![]()
![]() は部分積分法により、次のように計算される。
は部分積分法により、次のように計算される。
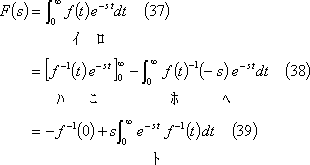
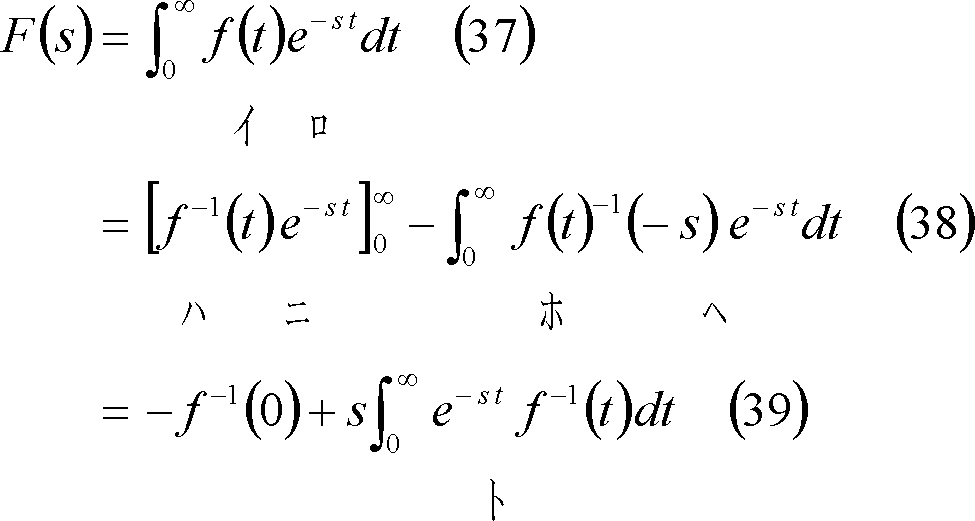

第5図 積分形関数
[例] 時間関数が電流
![]()
![]() である場合は、(40)式から次式となる。
である場合は、(40)式から次式となる。
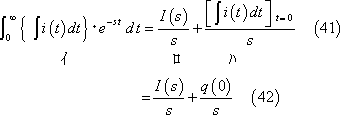
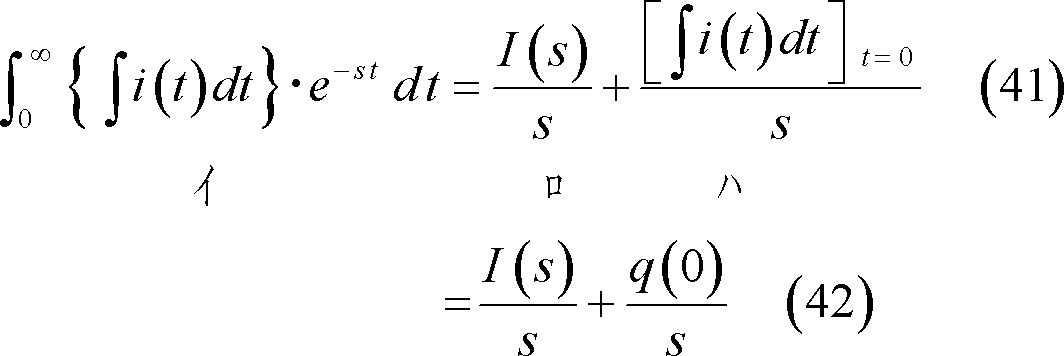
② 時間関数が2階の積分形である場合は、
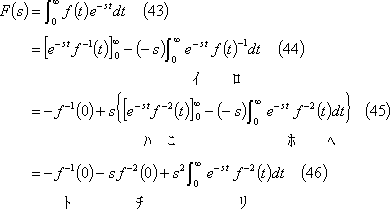
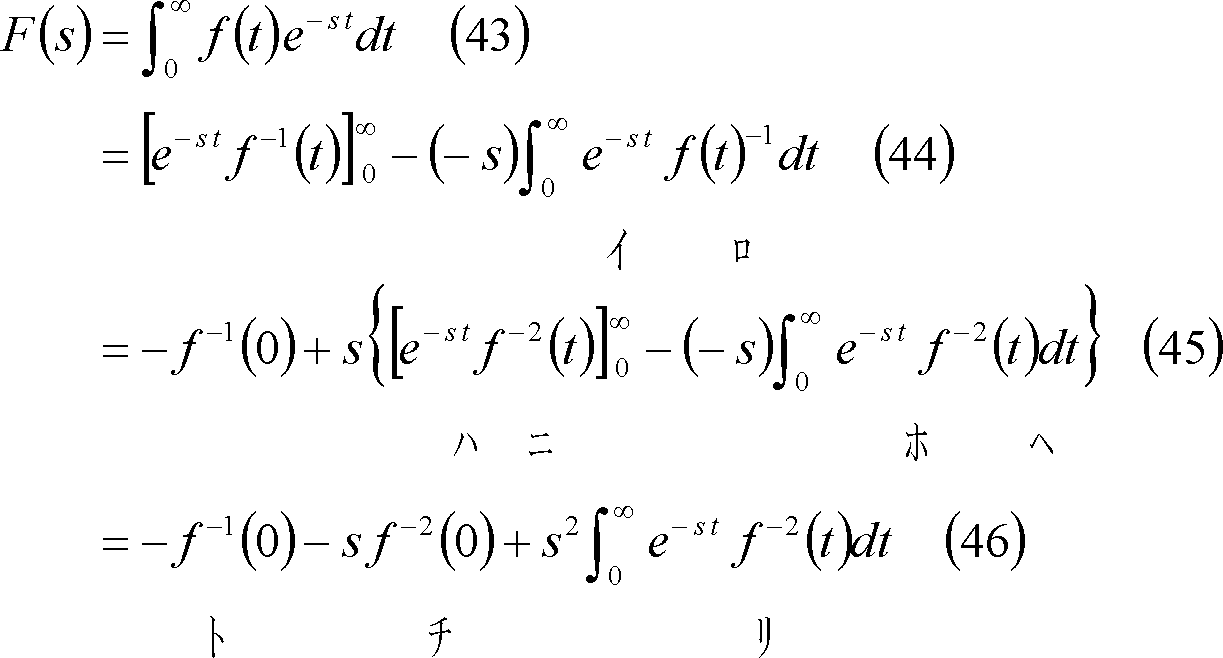
なお、ラプラス変換の表記には次のような方法もある。
ここに、
![]()
![]() は「
は「
![]()
![]() の後にある
の後にある
![]()
![]() の中にある時間関数をラプラス変換したもの」を表す。
の中にある時間関数をラプラス変換したもの」を表す。
![]()
![]() はラプラス演算子(ラプラシアン)と呼ぶ。これまでの例でいえば、
はラプラス演算子(ラプラシアン)と呼ぶ。これまでの例でいえば、
のように表記する。
これまでに扱った関数をまとめると第1表のようになる。
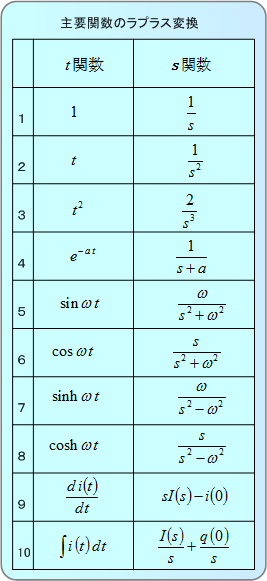

すべての時間関数に共通なラプラス変換の性質を第2表に示す。


(1) ラプラス変換の定義を知る。参考:計算イメージ
(2) ラプラス変換計算法の仕組みを理解する。第2図。
[計算手順] ① 電圧方程式 ② ラプラス変換 ③ s回路計算 ④ ラプラス逆変換 の4ステップ。
(3) 電気工学で使用頻度の高い時間関数(主要関数)について、t関数からs関数に変換する計算の方法を理解し、その結果をしっかりと記憶しておく。(第1表)
(4) ラプラス変換に関する諸法則(基本法則)について、具体的な時間関数への応用の方法を知っておく。
