（１）コンデンサＣ に流れこむ電流ｉは、
ｉ の正方向を印加電圧ｖ の正方向と同方向に選べば、次式となります。
(0)
（２）正弦波交流電圧が加わっている場合にコンデンサに流れる電流。
第１図（ａ）のように、コンデンサＣ に直流電圧Ｅ が加えられている状態、例えば時間ＡＢ区間では、直流電圧は電圧の値と方向が時間的に変化しないので、コンデンサの電荷に時間的変化が生じません。したがって、直流電圧が印加されている状態ではコンデンサには電流は流れません。
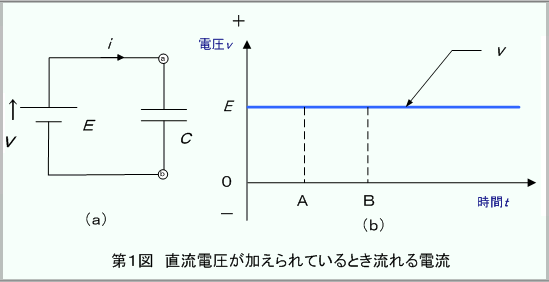
コンデンサへ直流電圧を印加した直後に、どんな現象が起こるのか調べてみましょう。
第２図（ａ）において、Ｃ の電荷をｑ 、回路を流れる電流をｉ とし、ｉ の正方向を印加電圧ｖ
と同方向に選べば、
いかなる瞬時においても次の（１）式が成立し、同式をｑ を使って表すと（２）式となります。
(1)
(2)
（１）、（２）両式は回路の電圧方程式と云います。
ここで、Ｃ の電荷がはじめ零で、ｔ ＝０の時、スイッチＳを閉じたとして、（２）式でｑ を求めると、（３）式が得られます。
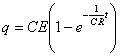(3)
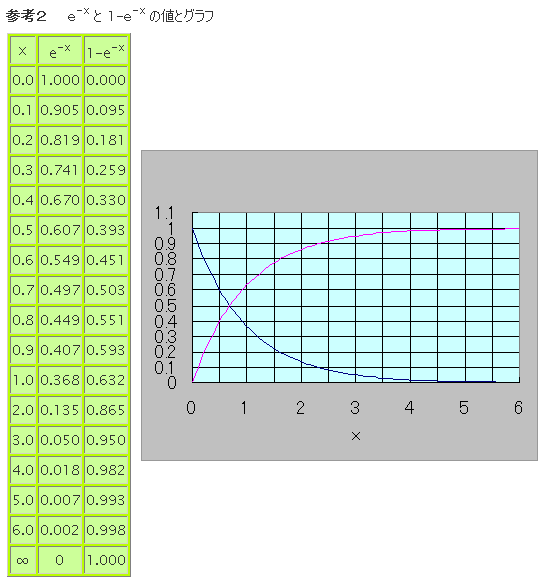
このように、コンデンサに電荷を蓄えることを充電と云います。（３）式は充電の時間的な経過を表しています。
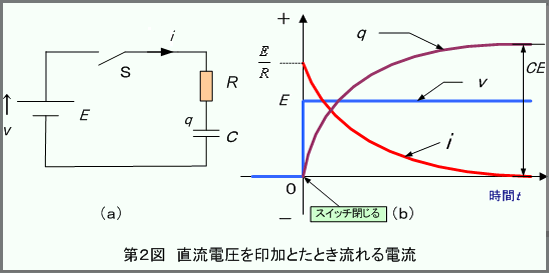
（３）式より、ｔ ＝０の時の電荷q (0)が零で、ｔ ＝∞のときの電荷q
(∞)はＣＥ となります。
また、コンデンサに流れる電流ｉは、電荷ｑとの関係から、（３）式を時間で微分すればよく、次のように求められます。
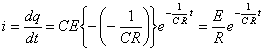(4)
ｔ ＝０における電流ｉ (0)は、（４）式でｔ ＝０とおけばよく、
となります。
ｔ ＝∞のときの電流ｉ (∞)は、
なので、零となります。
したがって、ｉ は（ｂ）図に示すように、電圧印加の瞬間がで、以後、時間が経過するにつれて次第に減少し、最後には零となります。
（３）式と（４）式において、ＣＲ は時定数Ｔ と呼ばれ、電流の時間的変化の目安になる量です。Ｔ
が大きいほど電流は緩やかに変化（(4)式の場合は減少）します。
【考察１】 どうしてこのような電流の流れ方をするのか考えてみよう。
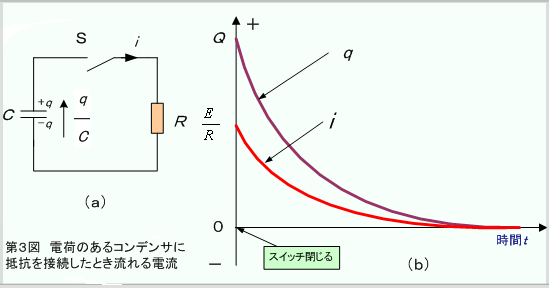
第３図（ａ）のように、電荷Ｑ が蓄えられているコンデンサＣ にスイッチＳを閉じて抵抗を接続してみると、Ｃ
から電荷の放出がはじまり、抵抗へ電流が流れます。このように、Ｃ から電荷が外部に出て行く現象を放電と云います。この場合の回路の電圧方程式は、電流ｉ
の正方向を図のようにＣ の端子電圧と同方向にとれば、
(5)
となります。この場合、ｑ とｉ との関係は、（６）式となるので、この関係を（５）式に代入することで（７）式が得られます。
(6)
(7)
ｔ ＝０のときＳを閉じると、この時の電荷ｑ (0)＝Ｑであり、これを条件として（７）式の電圧方程式を解くと、（８）式のように電荷
ｑが求まります。
(8)
放電電流ｉは（８）式の結果を（６）式へ代入して、（９）式のように求められます。
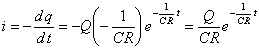(9)
ここで、Ｑ／Ｃ は、Ｓを閉じる前にＣ の端子に現れていた電圧で、これをＥ とおけば、（９）式は、
(10)
となります。ｑ およびｉ のグラフは、（ｂ）図のようになります。
【考察２】 ｑ とｉ になぜこのような変化が起こるのか考えてみましょう。
参考１ ａを定数とすれば、
(11)
